Algebraic Notation Algebraic Notation

Writing AND , OR , NOT etc. is long-winded and tedious. We generally use a more compact notation:

xy means x AND y
x+y means x OR y
[`x] means NOT x
x Åy means x XOR y

The operations can be combined to form algebraic expressions representing logic functions.

Examples:


xy + yz + zx
is the majority voting function from the previous lecture.


x(y+z)
means


x AND (y OR z)

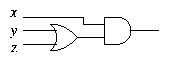
w1l2p1.png


x(
y + z
 
 )
means


x AND NOT (y OR z)

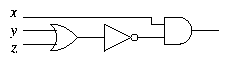
w1l2p2.png

and also


x AND (y NOR z)

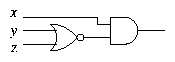
w1l2p3.png

Multi-input Gates

The AND and OR operations can be generalized to take any number of inputs. Algebraically, we simply write xyz for the three-input AND of x, y and z. Similarly we write x+y+z for the three-input OR of x, y and z. In circuit diagrams we use the same symbols as before, but with additional input wires:

w1l2p4.png

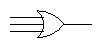
w1l2p5.png

The definitions of multi-input AND and OR are the obvious ones: AND is true if and only if all the inputs are true; OR is true if and only if at least one of the inputs is true.

Multi-input gates might be available as electronic components, if the number of inputs is not too large. Otherwise, an n-input gate can be synthesized from 2-input gates of the same type, e.g.

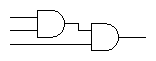
w1l2p6.png

Multi-input NAND and NOR gates also exist.

Exercise How many 2-input AND gates are needed to synthesize an n-input AND gate?

Algebraic Laws

The logical operations satisfy some algebraic laws, which can be used to rewrite expressions. x, y and z stand for arbitrary expressions.


x
 
=
x
(1)
x
x
 
=
0
(2)
xx
=
x
(3)
x +
x
 
=
1
(4)
x + x
=
x
(5)
x0
=
0
(6)
xy
=
yx
(7)
x1
=
x
(8)
x + y
=
y + x
(9)
x + 0
=
x
(10)
x(y + z)
=
xy + xz
(11)
x + 1
=
1
(12)
x + (y + z)
=
(x + y) + z
(13)
x(yz)
=
(xy)z
(14)
These laws can be verified by thinking about the ordinary meanings of AND , OR and NOT , or by truth tables.

The last two laws (technically, associativity of AND and OR ) justify writing xyz and x+y+z for the 3-input versions of the operators; it does not matter whether we interpret xyz as x(yz) or as (xy)z.

Example

To verify that x(y + z) = xy + xz we construct the truth tables for the left and right hand sides of the equation, considering them both as functions of x, y and z. The columns for x(y + z) and xy + xz are identical, indicating that the two functions are equivalent.


x
y
z
y + z
x(y + z)
xy
xz
xy + xz
0
0
0
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
1
0
0
0
0
0
1
1
1
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
1
1
0
1
1
1
1
0
1
1
1
0
1
1
1
1
1
1
1
1
1
Exercise In the same way, check that xy + x = x. Also try to derive this equation algebraically, using the laws on the previous slide.



File translated from TEX by TTH, version 2.78.
On 27 Jul 2001, 10:19.