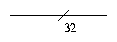Decoders and Multiplexers

Decoders and Multiplexers Decoders and Multiplexers

Decoders

A decoder is a circuit which has n inputs and 2ⁿ outputs, and outputs 1 on the wire corresponding to the binary number represented by the inputs. For example, a 2-4 decoder might be drawn like this:

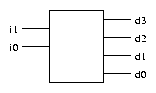
and its truth table (again, really four truth tables, one for each output) is:

i₁
i₀
d₃
d₂
d₁
d₀

0
0
0
0
0
1

0
1
0
0
1
0

1
0
0
1
0
0

1
1
1
0
0
0

We can immediately see that

d₃

=

i₁i₀
d₂

=

i₁
i₀

d₁

=

i₁

i₀
d₀

=

i₁

i₀

i.e. each of the d outputs corresponds to one of the four minterms.

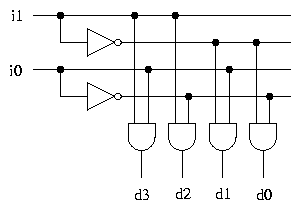
The Decoder Circuit

The following circuit generates all four minterms from two inputs, and implements the 2-4 decoder.

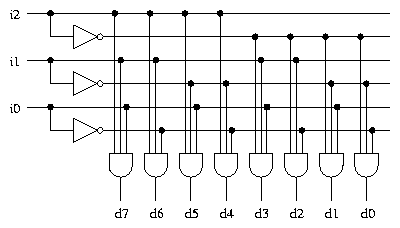
Larger decoders can be implemented in the same way. Here is a 3-8 decoder.

Traffic Lights with a
Decoder

Using a 2-4 decoder, the circuit which generates traffic light combinations is as follows.

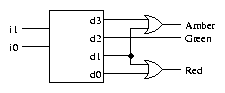
We no longer have to think about the problem of invalid inputs being presented to the circuit.

To complete the traffic light controller, we just need to make the inputs i₀ and i₁ cycle through the binary representations of the numbers 0Ľ3. We will see how to do this later in the course.

Decoders of various sizes are available as standard components.

Exercise The smallest possible decoder is a 1-2. How is this implemented?

Exercise How many components (inverters and 2-input AND gates) are needed to build an n-2ⁿ decoder?

Decoders with Enable

A standard decoder typically has an additional input called Enable.

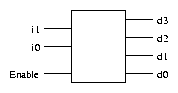
Output is only generated when the Enable input has value 1; otherwise, all outputs are 0. Only a small change in the implementation is required: the Enable input is fed into the AND gates which produce the outputs.

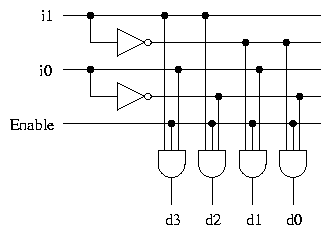
Many components have an Enable input which works in this way. Sometimes the Enable input is ``active high'', sometimes ``active low''.

Exercise How must the circuit be modified to make the Enable input active low?

Multiplexers

A multiplexer is a device which allows one of a number of inputs to be routed to a single output. Here is a 4-1 multiplexer.

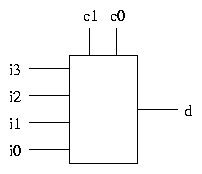
The control inputs c₀ and c₁ represent a 2-bit binary number, which determines which of the inputs i₀Ľi₃ is connected to the output d.

If c₁c₀ represents the number n in binary, then the value of the output d is the value of input i_n.

Multiplexers are useful in many situations. For example, in a CPU, data being written to memory might come from one of a number of sources - from a register, from the result of a calculation, etc - so a multiplexer would be used to select data from the appropriate source.

Another application is where we want to be able to choose one of several operations to carry out on some data - all the operations can be calculated, and a multiplexer can be used to select the desired result (more on this later).

Implementing Multiplexers

The implementation of a multiplexer is straightforward, and uses a decoder. Here is a 4-1 multiplexer.

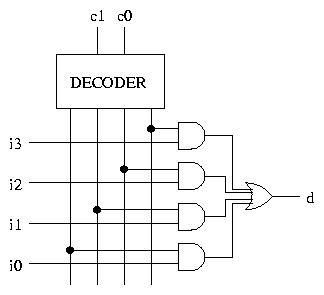
All the outputs of the decoder are 0, apart from one. The inputs c₁c₀ determine which of the outputs is non-zero.

All but one of the AND gates have 0 on one input and therefore output 0. The remaining AND gate has 1 on one input and i_n (where n is represented in binary by c₁c₀) on the other input. The output of this AND gate is the value of i_n.

The OR gate has 0 on all of its inputs apart from one, and has the value of i_n on the remaining input. The output of the OR gate is therefore the value of i_n.

Larger multiplexers can be implemented in the same way.

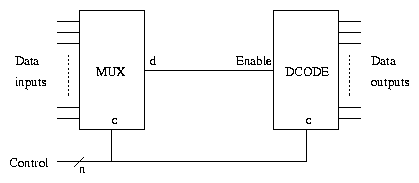
A Multiplexer Application

A multiplexer and a decoder can be used together to allow sharing of a data transmission line by a number of signals. In the following diagram, the Control input consists of n wires, and there are 2ⁿ data inputs and outputs. The Control input determines which of the data inputs is connected to the transmission line.

Exercise What does a 2-1 multiplexer do? How is it implemented?

Exercise How many control inputs does a 16-1 multiplexer have?

Multibit Multiplexers

The basic 2ⁿ-1 multiplexer is a switch, allowing one of 2ⁿ inputs to be connected to the output. Each input consists of a single bit.

It is often necessary to consider a group of wires as a single signal. For example, in a 32-bit microprocessor, all data is handled in blocks of 32 bits, which means that 32 wires are needed to carry a value from one part of the circuit to another.

A collection of wires which form a single signal is called a bus. In circuit diagrams, a bus is represented by a single line with a short diagonal line across it, labelled to indicate the width (number of wires) of the bus.

It is often necessary to use multiplexers to switch whole buses. In diagrams, we simply draw a multiplexer as usual, with buses of specified width as inputs and output.

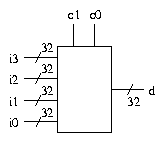
This example shows a 4-1 multiplexer on a 32 bit bus. Note that the control inputs are still individual wires. A 32 bit multiplexer can be implemented with 32 basic multiplexers, all sharing the same control inputs.

Multiplexers and
Logic Functions (1)

Any logic function of n inputs can be implemented with a 2ⁿ-1 multiplexer. For example, for a 2 input logic function, call the inputs x and y and the result r, and let the truth table be:

x
y
r

0
0
a

0
1
b

1
0
c

1
1
d

where a, b, c and d are each either 0 or 1. The following circuit implements this logic function:

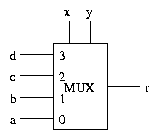
because x and y, when connected to the control inputs, select the correct row of the truth table.

Exercise How many logic gates are used by this implementation (if the multiplexer is fully expanded into gates)? How does this compare with the number of gates required to implement a logic function directly?

Exercise Show how each of the functions AND , OR and NOT can be implemented with a 2-1 multiplexer.

Multiplexers and
Logic Functions (2)

Any logic function of 3 inputs can be implemented with a 4-1 multiplexer and an inverter, as follows.

Let the inputs be x, y and z. Connect x and y to the control inputs of the multiplexer. For each combination of values of x and y, one of the following must apply.

The output is 0, regardless of the value of z.

The output is 1, regardless of the value of z.

The output is equal to z.

The output is equal to [`z].

For each combination of values of x and y, the multiplexer input which is selected by that combination is connected to either 0, 1, z or [`z], depending on which of the above cases applies.

Example: Majority voting

x
y
z
r

0
0
0
0
0

0
0
1
0
0

0
1
0
0
z

0
1
1
1
z

1
0
0
0
z

1
0
1
1
z

1
1
0
1
1

1
1
1
1
1

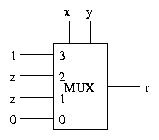Example: Parity

x
y
z
r

0
0
0
0
z

0
0
1
1
z

0
1
0
1

z

0
1
1
0

z

1
0
0
1

z

1
0
1
0

z

1
1
0
0
z

1
1
1
1
z

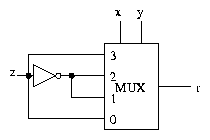
Multiplexer
Applications (2)

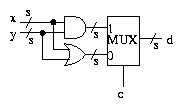
Using a multiplexer we can build a circuit which allows one of a number of operations to be chosen, and applied to the inputs. For example, here is a circuit which gives a choice between AND and OR .

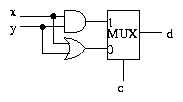
If c = 1 then d = x AND y. If c = 0 then d = x OR y.

For a choice between more operations, a larger multiplexer can be used.

The same idea can be used for operations on multibit words. For example, using 8 bit words, we just replace every wire (except the c wire) by an 8 bit bus:

In this circuit, the AND operation is extended to 8 bit words by operating on each bit position independently (and similarly OR ): for example 11010010 AND 01110110 = 01010010.

Multiplexer
Applications (3)

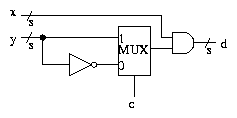
A similar example, which is relevant to the exercises in Lab Session 3, is calculating either x AND y or x AND (NOT y), where again x and y are multibit values.

These examples show how the ALU (arithmetic and logic unit) of a microprocessor can be implemented. The ALU is a component which can carry out a range of calculations on its inputs, including various standard arithmetic and logic operations. The choice of operation is made by setting control inputs appropriately; ultimately, the control inputs are determined by the instruction which the CPU is executing at any given time. We'll go further into this idea later in the course.

Demultiplexers

A demultiplexer is the opposite of a multiplexer. There is one data input, whose value appears on one of the data outputs, depending on the value of the control inputs. Here is a 1-4 demultiplexer.

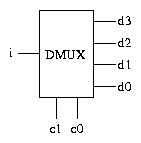
If the control inputs c₁c₀ represent the number n in binary, then the value of i is copied to output d_n. Depending on the details of the electronic implementation, the other outputs might be 0, or might be in a disconnected state.

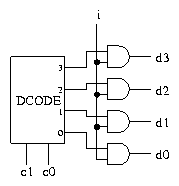
It is straightforward to implement a demultiplexer; the circuit uses a decoder in a similar way to the implementation of a multiplexer.

File translated from T_EX by T_TH, version 2.78.
On 27 Jul 2001, 10:19.