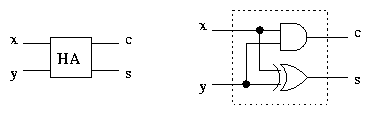Addition and Subtraction Addition and Subtraction

Addition

We want to be able to do arithmetic on computers and therefore we need circuits for arithmetic operations. Naturally, numbers will be represented in binary. We'll start with addition.

Addition in binary is just like addition in decimal. For example, here is the calculation for 13 + 6.


1
1
0
1
0
1
1
0
+
1
0
0
1
1
1
The result, 10011, is 19 in decimal as we expect.

In the calculation, every column (i.e. every digit position) is processed in the same way: we add two bits (from the numbers being added) and a carry bit from the previous column, generating the sum for that column (0 or 1) and a carry (0 or 1) to go to the next column.

In the first column, there is no previous column so the carry input is 0.

The carry output from the last column becomes the most significant bit of the result.

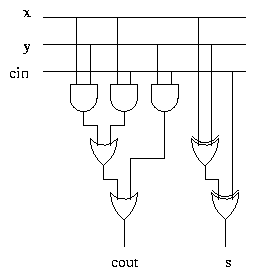
Designing an Adder

Here is the truth table for the single bit addition function. The numbers being added are x and y. The carry input is cin. The sum is s and the carry output is cout.


x
y
cin
cout
s
0
0
0
0
0
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
1
0
0
0
1
1
0
1
1
0
1
1
0
1
0
1
1
1
1
1
Notice that the cout and s columns, interpreted as a 2 bit binary number, simply represent the sum of the x, y and cin columns.

Exercise Draw Karnaugh maps for the s and cout outputs.

It turns out that cout is the majority voting function from Lecture 1, and s is the parity (or 3 input XOR ) function from Lecture 3.

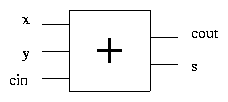
Implementing the Adder

We now know that


s
=
x Åy Åcin
cout
=
xy + ycin+ cinx
and therefore we can easily construct a circuit which implements a single bit adder.

w4l1p1.png

A single bit adder is usually represented as follows.

w4l1p2.png

Multi-Bit Addition

Addition of multi-bit numbers is achieved by chaining single bit adders together. For example, here is a four bit adder. The inputs are x and y, expressed in binary as x3x2x1x0 and y3y2y1y0, and the result is s, expressed in binary as s4s3s2s1s0.

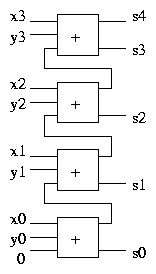
w4l1p3.png

The carry out from each adder is fed into the carry in of the next adder. The carry in of the adder for the least significant bit is connected to 0.

Note that if two n bit numbers are added together, the result can always be expressed in n+1 bits: if x < 2n and y < 2n then x+y < 2n + 2n = 2(n+1).

Half Adders

In effect we have directly implemented addition of three binary digits. Let's consider addition of just two digits, which is obviously more fundamental, even though it does not directly correspond to the original calculation.

Adding two bits x and y produces a sum s and a carry c:


x
y
c
s
0
0
0
0
0
1
0
1
1
0
0
1
1
1
1
0
We can see at once that c = xy and s = x Åy. Using one AND gate and one XOR gate we can implement a half adder, which we represent like this:

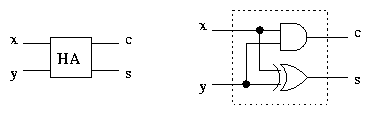
w4l1p4.png

As the name suggests, two half adders can be combined to produce a full adder.

Two Halves Make a Whole

The following circuit uses two half adders to implement a full adder.

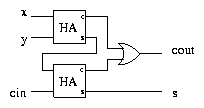
w4l1p5.png

Exercise Use a truth table to check that this circuit is correct.

This implementation of the adder uses 2 AND gates, 2 XOR gates, and 1 OR gate. Our original implementation used 3 AND gates, 2 XOR gates, and 2 OR gates. Somehow, splitting the adder into two half adders has saved an AND gate and an OR gate! This issue is explored by the following

Exercise The full adder circuit on Slide 3 calculates


s
=
(x Åy) Åcin
cout
=
xy + xcin+ ycin.
Recall that xcin+ ycin = (x + y)cin. Using this fact, modify the full adder circuit to remove one of the gates. Redraw the circuit from Slide 6, replacing each half adder with an AND gate and an XOR gate. Write down the equations which this circuit is calculating. You now have two circuits, one of which calculates xy + (x + y)cin and the other of which calculates xy + (x Åy)cin. Why are these two formulae equivalent? Check it with truth tables, and also try to produce an explanation. The equations calculated by the second circuit (using the half adders) use 6 logical operations. Why does the circuit itself only contain 5 gates?

Ripple Carry

The electronic implementations of logic gates do not work instantaneously - when the inputs change there is a short delay, perhaps a few nanoseconds, before the outputs change. When a multi-bit adder is constructed from single-bit adders, the calculation of each bit of the result involves more delay than the calculation of the previous bit. This is because the carry bits have to propagate all the way along the circuit. For this reason, the multi-bit adder we have presented is known as a ripple carry adder. The longer the sequence of bits being added, the longer the delay.

The delay caused by the ripple carry design doesn't matter for small adders, but when adding longer words in a fast microprocessor, it can become very significant. More complex adder designs exist, which use various shortcuts to calculate carry bits without the need to propagate them along the whole word. We won't consider such lookahead carry designs in this course - wait for next year, or consult the books.



File translated from TEX by TTH, version 2.78.
On 27 Jul 2001, 10:19.