Contents

kernelkmeans.m

From A First Course in Machine Learning, Chapter 6. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] Kernel K-means

clear all;close all;

Load the data

load ../data/kmeansnonlindata

Plot the data

figure(1);hold off
plot(X(:,1),X(:,2),'ko');

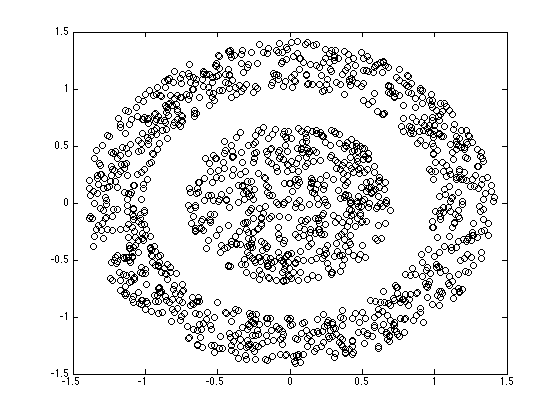
Compute the kernel

N = size(X,1);
Ke = zeros(N);
gam = 1;
for n = 1:N
    for n2 = 1:N
        Ke(n,n2) = exp(-gam*sum((X(n,:)-X(n2,:)).^2));
    end
end

Run Kernel K-means

converged = 0;
% Assign all objects into one cluster except one
% Kernel K-means is *very* sensitive to initial conditions.  Try altering
% this initialisation to see the effect.
K = 2;
Z = repmat([1 0],N,1);
s = sum(X.^2,2);
pos = find(s==min(s));
Z(pos,:) = [0 1];
di = zeros(N,K);
cols = {'r','b'};

Plot the assignments

figure(1);hold off
for k = 1:K
    pos = find(Z(:,k));
    plot(X(pos,1),X(pos,2),'ko','markerfacecolor',cols{k});
    hold on
end

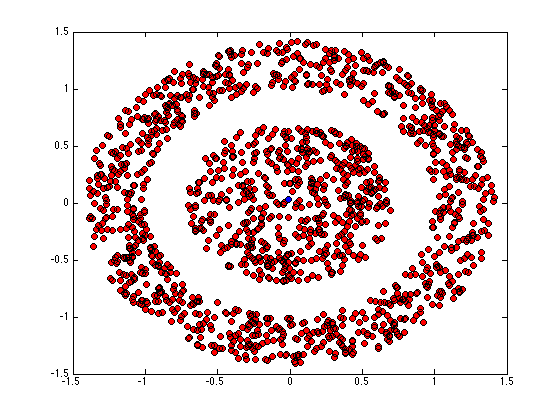
while ~converged

    Nk = sum(Z,1);
    for k = 1:K
        % Compute kernelised distance
        di(:,k) = diag(Ke) - (2/(Nk(k)))*sum(repmat(Z(:,k)',N,1).*Ke,2) + ...
            Nk(k)^(-2)*sum(sum((Z(:,k)*Z(:,k)').*Ke));
    end
    oldZ = Z;
    Z = (di == repmat(min(di,[],2),1,K));
    Z = 1.0*Z;
    if sum(sum(oldZ~=Z))==0
        converged = 1;
    end

Plot the assignments

    figure(1);hold off
    for k = 1:K
        pos = find(Z(:,k));
        plot(X(pos,1),X(pos,2),'ko','markerfacecolor',cols{k});
        hold on
    end

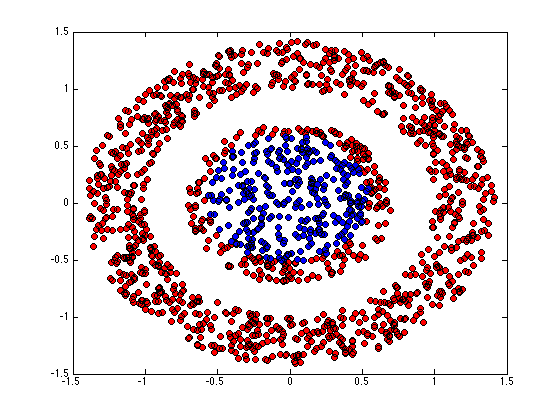
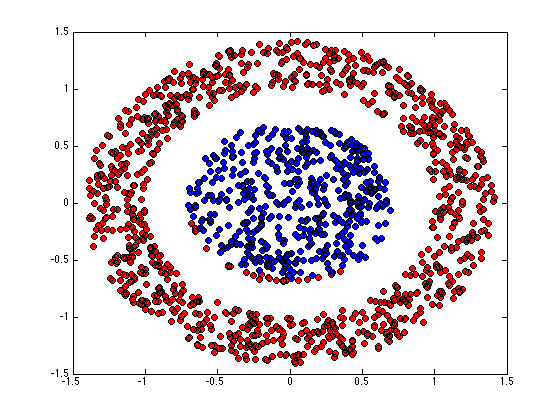
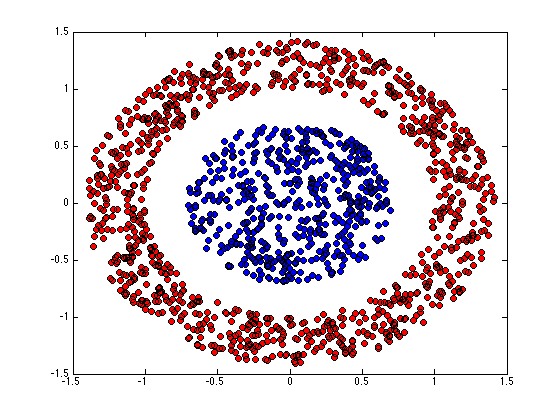
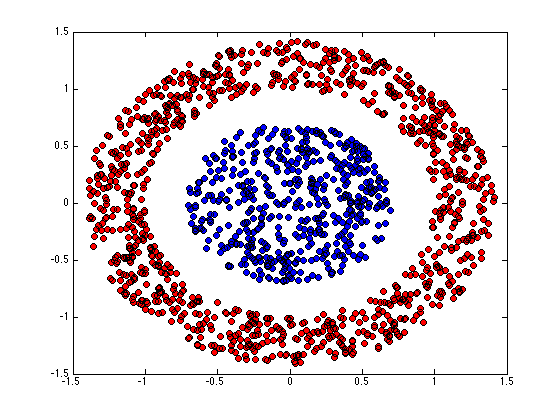
end

Published with MATLAB® 7.13