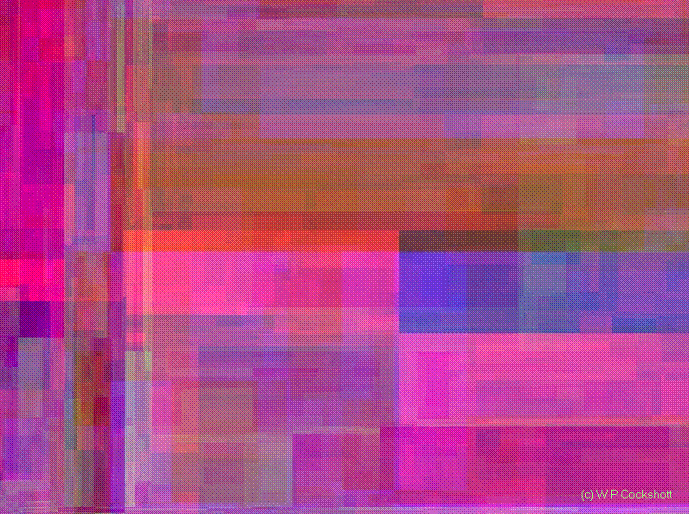 fs-64-100
fs-64-100
The first set of images are coloured random fractal patterns. They were generated with a scientific intent, we needed to project fractal patterns onto smooth surfaces in order to get better triangulation off them when using stereo range finding. We had previously used Gaussian noise patterns, but I thought that coloured fractals should be better suited to our range mapping process which worked by pyramid decomposition of left and right stereo images. The coloured patterns that I generated turned out to be much more attractive to look at than Gaussian speckle patterns.
The picture above was generated using a recursive subdivision of each colour plane into rectangles. Rectangles are repeatedly divided into two rectangles a, b on a random position along either the vertical or horixontal axis. As this is done a random offset the mean of whose probability density function is proportional to the square root of the area of the rectangle is added to the brightness level of a and subtracted from the brightness of b.

The picture above achieves a more painting like effect by selecting random dividing line P Q for each rectangle as before, but then raising or lowering the dividing line in brightness space by adding a random variable with mean 0 and σ ≈ k |PQ|. The two sub rectangles then become inclined planes in brightness space which are further subdivided.


When working with such fractals one can vary the degree of contract by altering the constant k which controls the degree of randomness in the colour space. The image on the left has a larger k than that on the right.



The next series of images are the result of performing warping operations on source images. The warps in question are ones that map the entire Euclidean infinite plane into either a rectangle or an elipse. The distance compressing warp that I use is d(x )=1-1/(1+x) which tends to 1 as x tends to infinity.
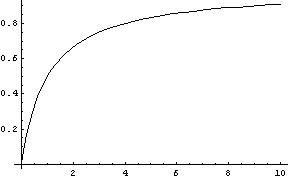
Thus an position x, y in the positive Cartesian quadrant can be mapped to a point d(x),d(y) in the unit square.
If we imagine the plane being tiled by repeated occurrences of a photograph we can then squash the infinite tiles surface into a small rectangle.

The picture above illustrates this infinite tiling process applied to to the fractal image fs-64-100 shown above.
|
|
|
|
|
|
|
|
|
|
|
|
The following transforms have enhanced symmetry with infinity all round the margin of the disk. The mapping used to derive them is based on the use of polar coordinates with an inverse harmonic transform on the radius.

Symmetries and exchange relations An artwork on the subject of money and exchange, featuring the monetary system introduced by the British colonialists to Nigeria, the Kola nut, and its most famous commodity derivative.
The image is produced by a sequence of unitary rotations and scale preserving translations in the non Euclidean space of the Poincare disk. To read more about this click here .
![]()

Ellipse Kunst from an original image by Lee Cockshott
![]()

Fovea
A harmonic polar tiling of the iconic Lena image, with is a metaphor for how the fovea is much more sensitive to detail than the periphery of our eyes


If we apply the process to very simple and regular patterns like national flags we can get an intuitive understanding of the geometrical process underlying this. Take the crosses of St George and St Andrew and we get:
|
St Andrew’s Cross |
St Andrew’s Poles |
|
|
|
|
St George’s Cross |
St George’s Parallels |
|
Union Flag |
Ever Wider Union Flag |
In the harmonic warps used above, the spatial dimensions are treated separately so that we are treating the underlying space as a manhattan rather than a Euclidean space. The street lines of the Manhattan grid would be preserved as parallel lines as is show by the picture St George’s parallels. Lines at 45 degrees are transformed into curves , though within the transformed Manhattan metric these are still parallels that meet only at infinity – this is illustrated by the St Andrews poles.
What happens if we transform the warp so that the infinities, instead of being at the edges of the picture, are shrunk to the 4 polar cardinal points of the compass? We get something very like the Hyperbolic space of General Relativity. In hyperbolic geometry the sum of the angles of a triangle are always less than 180 degrees. This can be represented in the Euclidean plane as a disk with infinity at the circumference of the circle, this is known as the Poincare disk. A problem with this representation of hyperbolic space is that straight lines map to circles in the Poincare disk. The X and Y axes correspond to circles of infinite radius so that they remain straight lines, but a line offset from the origin will always be a circle.
We can map positions in the disk to x, y coordinates in Cartesian space by finding the circles which cut the x and y axes at 90 degrees and pass through a given point. Let these intercepts with the x and y axes be called hx , hy and the original coordinates within the Poincare Disk as px, py. Then the two are related by the rules:
If we subsequently perform an inverse harmonic map on hx, hy we end up with positions in Cartesian 2 D space.
What does this do to straight lines ad different angles?
Well we can look again at the national flags. Note that I have retained the original aspect ratios for the flags after the inverse harmonic map so the Poincare disc becomes an ellipse.
|
The original cross of St Andrew survives in the midst of polar collapse on either side |
|
|
St George’s Ellipses |
|
|
|
The rather more sinister image of the Union flag on the Poincare ellipse |

Escher’s chess board

Htt Chess

HYP Chess

Expanding Chess

Belly world

Chrysler
Framed
Fractal Limit
![]()