Demography and the falling rate of profit
Allin Cottrell and
Mailing address
Dr W P Cockshott
Department of Computing Science
17
Abstract
We discuss the original formulation of the theory of the
falling rate of profit by Marx and the criticisms of the theory’s micro-foundations
by Roemer. We then counterpose to this an alternative
macroeconomic interpretation in which the falling rate of profit is driven by
demographic factors. We follow this up with an examination of why the
assumptions made in Roemer’s analysis are empirically unjustified. In
particular we criticize his use of the average rate of profit rather than the
monetary interest rate as the regulator of investment decisions. We conclude
with an examination of the social implications of a declining rate of profit.
“…the difficulty which has hitherto troubled the economists, namely to explain
the falling rate of profit…” (Marx,
Capital III, p. 230)
The concept of a tendency for the rate of profit to fall was a common theme in classical political economy. Smith, Ricardo and Marx all held such a theory. However, their grounds for believing in this tendency were quite various. Smith thought in terms of accumulation leading to an increase in competition between capitals, hence driving down prices and profits. Ricardo dismissed this as a confusion – competition between capitalists influenced the distribution of profit, not its overall amount – and held a theory whose motor lay in the confrontation between rising population and diminishing returns in agriculture. Marx’s theory was in a sense more akin to Smith’s – at least insofar as it had nothing to do with diminishing returns – but it was quite distinct.
We distinguish three elements in Marx’s writings that are particularly relevant to our topic. The first we call the “main argument”: this is the argument Marx set out at length (and which appears in Capital I, his notebooks of the 1860s, and Capital III) to the effect that the rate of profit must tend to fall due to an increase in the organic composition of capital, an increase itself driven by the search for maximum profit on the part of capitalists. The second is a brief coda to the main argument (appearing towards the end of Chapter XV of Capital, III) but worthy of mention in its own right in view of its relevance to later discussions of the TRPF. We call it the “micro-macro bridge”. The third element is what Marx calls “absolute overproduction of capital”: this element forms the basis for the revised TRPF theory that we defend below.
In outline, our argument is as follows. First, Marx’s “main argument” is flawed, and vulnerable to the Okishio critique. Specifically, Marx’s micro-macro bridge is invalid. Nonetheless, the Okishio critique is questionable on various grounds and we explore some of these. Second, it is possible to construct a revised version of the TRPF theory, which is not vulnerable to the Okishio critique, on the basis of Marx’s concept of absolute overproduction of capital. And this construction is worthwhile, because the underlying concept is now more relevant than in Marx’s day and promises to become increasingly relevant over the 21st century.
We begin by sketching Marx’s main argument, for reference. The argument may be expressed thus:
1. It is an inherent, intrinsic feature of capitalism that capitalists are driven to seek maximum profits.
2. While profits can be gained in many ways, the most fundamental means of augmenting profit in developed capitalism is via increases in the productivity of labour.
3. The enhancement of the productivity of labour involves workers working with an increased “mass” of machinery or means of labour, and working up a larger quantity of materials per unit time.
4. Although the value of the means of labour, materials, etc (in Marx’s terminology, constant capital) will not generally increase in full proportion to the “mass”, it will nonetheless increase, and faster than the variable capital. The organic composition of capital tends to rise.
5. A rise in the organic composition of capital lowers the rate of profit, other things equal.
6. Other things cannot be expected to remain equal. The same increase in the productivity of labour, driven by profit-seeking, that expresses itself in a rising organic composition, also expresses itself in a rise in the rate of exploitation, which by itself raises the rate of profit.
7. Nonetheless, as a long-run tendency, the increase in organic composition must outweigh the increase in the rate of exploitation, in its effects on the rate of profit.
Most critics of Marx’s main argument have not questioned points 1 or 2 above, and neither will we.
Point 3 is perhaps more questionable. Certainly there are many examples of technological change that conform to this pattern: the switch from fluvial transport to railways, or from handlooms to machine ones, but there are also counterexamples. Sometimes, as for instance in the move from metal casting to plastic moulding for many uses, the more advanced process accomplishes its results more cheaply while deploying a lesser “mass” of means of production. But let’s accept point 3 as broadly correct, at least for the sake of argument (strengthen this statement?). Similarly for point 4: this may not always be true, but it is at least plausible and we will not question it here.
Points 5 and 6 are certainly correct within Marx’s conceptual framework.
That leaves point 7, the primary locus of controversy. To expose the issue here, it may be useful to write down the relevant equations. Marx’s rate of profit (here denoted by r) is the ratio of surplus value (s) to the sum of constant capital © and variable capital (v):
r = s / (c + v)
The organic composition of capital is the ratio c/v and the rate of exploitation is the ratio s/v. We can write
r = [s/v] / [(c/v) + 1]
which makes it plain that an increase in c/v lowers the rate of profit and an increase in s/v raises it.
If the pursuit of profit (via the pursuit of higher labour productivity) has the effect of raising both c/v and s/v, does that not leave the overall effect on the rate of profit indeterminate? Neither s/v nor c/v has any obvious theoretical upper bound. Why does Marx talk in terms of a basic tendency for the rate of profit to fall due to rising c/v, and treat rising s/v as merely an “offsetting factor”? Why not a tendency for the rate of profit to rise due to rising s/v, with the increase in c/v treated as an offsetting factor? (Or no “basic tendency” at all, just an indeterminate outcome.)
Marx clearly had an ideological investment in the idea that the falling rate of profit was primary. This proposition licensed the conclusion that “the real barrier of capitalist production is capital itself” (Capital, III, p. 248). The very process that constituted capitalism’s historical “justification” – namely, its development of the productivity of social labour to an unprecedented level – was at the same time the source of a falling rate of profit, which places a roadblock in the way of further development.
If the only reason Marx had for asserting the primacy of the tendency of the rate of profit to fall was that it fit well with his ideological agenda, one could accuse him of intellectual dishonesty. That is too harsh. It seems clear that he had a strong theoretical hunch or intuition that the rise in c/v must outweigh the rise in s/v. A further manipulation of the rate of profit may help here:
r = [s/(s+v)] / [c/(s+v) + 1]
The ratio s/(s+v) is not exactly Marx’s rate of surplus value, but it is a closely related magnitude with an upper bound of 1.0, namely the fraction of the total social working time during which workers perform surplus labour, or generate profits for their employers. Similarly, c/(s+v) is not exactly Marx’s organic composition, but it is a closely related quantity which seems to have no upper bound, namely the ratio of the value of constant capital to the total “living labour”. Looking at this variant of the rate of profit equation it becomes easier to share Marx’s intuition. Suppose the ratio s/(s+v) is driven to its maximum (wages are effectively zero; the workers “live on air”, as Marx puts it). In that case any rise in the ratio of constant capital to current labour is bound to lower the rate of profit. It then seems plausible that as s/(s+v) gets closer to 1.0 it will become increasingly difficult to find an offset on this account for an ongoing rise in c/(s+v), or in other words a rising rate of exploitation can’t keep capitalism out of trouble for ever.
The relevant question though is whether capitalists seeking to maximize their rate of profit would act so as to raise c/(s+v) sufficiently to lower the overall rate of profit. Okishio and Roemer have argued that they would not. Roemer lays considerable emphasis on the need for a sound microeconomic foundation for discussions of the rate of profit. The falling rate of profit is a macro-economic phenomenon, but it derives, he argues from the decisions of individual capitalists unaware of the macroeconomic consequences of decisions that they make. From this he argues that we have to examine what are plausible decision making criteria for individual capitalists when making investment decsions. The thrust of his analysis is that if capitalists take the current set of prices and profit rates as givens, then, any decisions that they make on technical changes which are more profitable to them personally, will also be more profitable to the capitalist class as a whole and, in consequence, will tend to raise the aggregate rate of profit for the whole economy. This theoretical project amounts to the search for an adequate microfoundation for the theory of accumulation.
Our approach comes from the opposite direction. We shall start from certain propositions about macro-economic magnitudes - population growth, the share of profits going as accumulation, the rate of technical change - and then draw conclusions about the trajectory of profit rates.
The Macro-economic Argument
When discusssing the rate of profit in value terms we are dividing a quantity of profit by a stock of capital. Profit can be thought of as a flow of value and as such its dimension its units are person hours/annum, which in dimensional terms is just persons since the hours/annum just give us a scalar. Thus the annual flow of profit when measured in value terms corresponds to a certain number of people - the number of people whose direct and indirect output is materialised in the goods purchased out of profits.
We divide this by a stock of capital whose units are person hours, thus the dimension of the annual value rate of profit is given as persons/(persons x time), which cancels out to time-1 . As such it expresses the potential expansion rate per year of a sum of capital. Obviously an analogous dimensional reduction could be achieved if we used Euros as our unit rather than person hours. Again we would come up with a dimension of time-1.
This dimensional issue is obscured in the classical discourse which talks in terms of a production cycle. In this the components of capital c+v are treated as sums of value as is the profit, and the time dimension is abstracted from since every thing is thought of as taking place over a single cycle. Capital is advanced on wages and means of production at the start of the cycle, at the end of the cycle the means of production and labour power have been used up and we are left with a product whose value replaces the advanced capital with a profit. Since there is only one production cycle the rate of surplus value s/v and the rate of profit s/(c+v) appear dimensionally identical
as simple scalars.
The whole debate in Okishio and Roemer is cast within the context of a choice over techniques, and whether any rational choice of techniques by a capitalist will result in techniques being chosen that will lower the rate of profit. This is a fundamentally mistaken starting point, although there are interesting issues raised by them and we will return to these later in our argument. Instead one should focus on what the rate of profit tells us. It tells us something about the potential rate of expansion of capital stocks. It sets an upper limit on the rate of expansion that can be achieved out of internal funding - the rate of capital growth that will be achieved if all profit is reinvested.
The focus of the analysis should be on how this rate of expansion will change over time if capital actually is reinvested. If we answer this question we can then go on to look at the circumstances
under which capital might be reinvested and also look at the consequences of capital not being reinvested.
If we approach the time evolution of the rate of profit from the standpoint of capital accumulation, then the issue becomes simpler. Initially we will assume that all measurements are performed
either in labour hours, or what amounts to the same thing in a monetary unit of account whose labour hour equivalent does not change from year to year. Let us further assume that all profits are reinvested. Thus a 5% rate of profit will imply a 5% growth per annum of the capital stock. Let us also assume at first that the division of value added between wages and profit remains unchanged over time.
This means that total profit per year will be a constant multiple of total wages per year. Under these circumstances it is clear that the rate of profit will fall over time if rate of growth of wage income is less than the rate of profit, and the rate of profit will rise if the rate of growth of wage income is higher than the rate of profit.
We then focus on the determinants of the rate of growth of wage income - measured in labour hours per annum. The dimensions give it away, since wage income in these terms corresponds to a number of people - the number of people whose direct and indirect labour supports
the employed population. The rate of growth of wage income comes down to the rate of growth of the working population ( given the assumption of a constant rate of surplus value ). The appropriate focus for analysis of the falling rate of profit is not technological choice but historical demography.
Once the argument is on this terrain one has to ask what determines the rate of growth of the working population. There are clearly two components that are important :
1. The natural rate of population growth.
2. The fraction of the total population that is employed as wage labourers under capitalist relations of production.
Economies undergoing transition from peasant farming to capitalist industry typically have a rapid rate of growth of the working population from both factors. The birthrate tends to be high and infant mortality falls during the transition from peasant agriculture to capitalist industrial economy. This gives a rapid rate of natural population increase. At the same time the fraction of the population employed as wage labourers rises to give a high compounded rate of growth of the employed population.
In a mature capitalist economy things are different, although infant mortality continues to fall, this is offset by a falling birth rate, which in many advanced capitalist economies falls below replacement level. At the same time the share of capitalistically employed wage labour in the population tends either to plateau or even to fall. The result is a relatively stagnant or declining capitalistically employed population.
If we assume that the rate of growth of the employed population is fixed then the effect is that the actual rate of profit tends towards the rate of growth of the employed population:


Figure 1, profit rate under constant population growth
In the graph above we start out with an initial rate of profit of 25% and have the population growing at 5%. All profits are reinvested so the rate of profit on capital tends towards 5% as well as this is the only rate at which the rate of growth of the capital stock will equal the rate of growth of the population.
If we take a more realistic model as shown in Figure 2, where the rate of growth of the population declines with time, then the rate of profit chases the rate of population growth downwards.
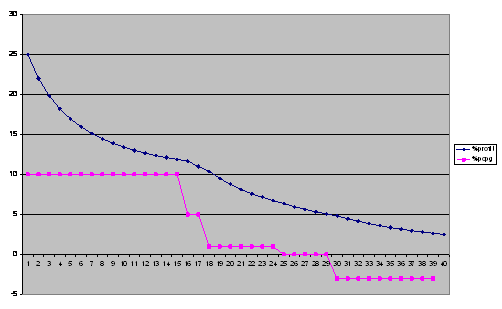
Figure 2 profit rate under declining population growth
These cases have used an assumption of fixed proportions of wages and profits. What will be the case if we assume that wages fall relative to profits with time.
We again simulate the effect of profits being reinvested with a constant 5% growth of the employed population but this time with a 5% decline in the value of the real wage each year.
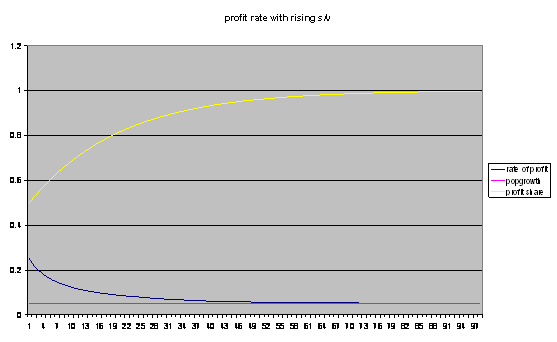
Figure 3, effect of a rising profit share
We see that the profit share in net value added heads up towards unity, but that this only serves to delay the equilibration of the profit rate at 5%. Again we find that the rate of population growth is the determinant of the long run rate of profit.
We have up to now assumed that all profits are accumulated. What happens if a smaller portion of profits are accumulated?
What if population grew at 5% a year and half of all profits were accumulated?
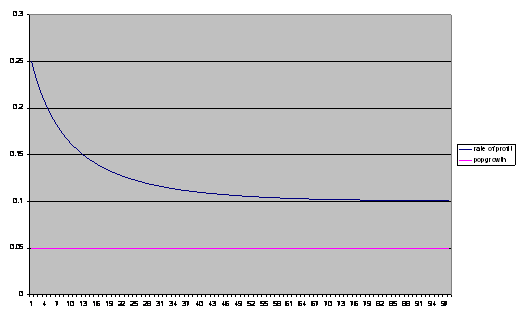
Figure 4, effect of lower accumulation rates, 50% in this case.
As the graph above shows, the result would be that the profit rate would tend towards 10% instead of 5%, because this is the rate of profit that would keep capital stock and working population growing at the same rate. In the example above the profit share in net value added is held constant. In general we can conclude that the equilibrium profit rate will be given by p/i where p is the rate of employed population growth and i is the investment share of profit. However if the employed population is static or declining, then for any positive i, the equilibrium rate of profit will be zero. In the above we are implicitly assuming that 50% of profits are used to fund capitalists personal expenditure rather than investment.
Countervailing factors
Technical change
Investment in new plant and equipment can be expected to improve production techniques and reduce the prices of capital goods. Under these circumstances the value of the stock of invested capital will depreciate. This will tend to slow the growth of the capital stock. At the same time, it will result in losses on the capital account to firms whose assets have depreciated. If we take these into consideration when calculating profits we find two opposite effects. The depreciation of capital stocks slows down the growth of stocks which tends to mitigate any decline in profit rates. Conversely, the losses on the capital account tend to directly reduce profits.
We simulate this in the following example where we assume that all net profits are invested. Population grows 5% a year for the first 30 years before gradually falling below replacement rate. For the first 50 years productivity grows 3% a year leading to a 3% depreciation per annum of the capital stock. Then for a period of 20 years the rate of technical change accelerates to 7% a year before falling back to 2% a year.
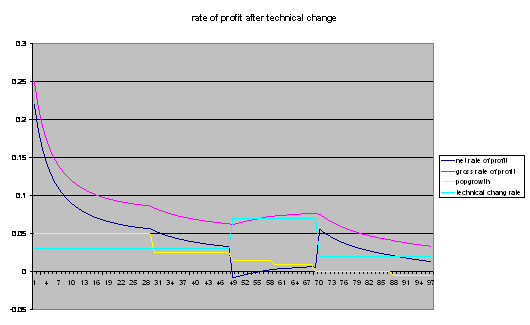
Figure 5 effect of technical depreciation
When technical change accelerates the net rate of profit declines sharply as the losses on capital account kick in, followed by a period during which they recover. This recovery occurs because the organic composition of capital falls when the net rate of investment is insufficient to keep up with the growth of the working population. A slowdown in technical change allows net profit rates to rise for a period before tending back towards equilibrium. In the presence of technical change, it is still the rate of growth of the working population that governs the long run rate of net profit.
Falling investment
Let us now look at the effect of falls in investment on realization and thus on profit rates using Kaleckian arguments. Up until now we have only looked at the effect of varying the share of investment in total profits keeping total profits unchanged under such a change. However we know from Kalecki, that total profits are casually determined by the sum of current capitalist consumption plus net investment. If workers neither borrow nor save, then investment expenditure plus capitalist consumption limit the sum of realizable profit.
To analyse this in more detail let us assume that capitalist consumption is given by some fraction of the average profits over the last few years. Thus capitalists are assumed to adjust their expenditure to their long run income, their savings buffering them from short term income falls.
In dimensional terms, capitalist consumption as flow of value, has dimension person hours / hour = persons. In value terms it represents the number of people directly and indirectly meeting the needs of capitalist consumption. If we assume that the rate of surplus value is 100% then for each person employed producing goods and services for capitalist consumption, a further person will be employed producing wage goods. Similarly for each person employed making net investment goods, a total of two people will be employed, one of whom will be making wage goods. Thus total employment will be 2 x (capitalist consumption + investment ). This will be limited above by the employable workforce, whose growth we have been modeling up to now, but it can fall short of the employable workforce if investment and capitalist consumption are too small. Let us construct a new simulation in which we allow for the possibility of unemployment.
In this model we assume that the labour force grows, stabilizes and then finally falls. We assume that accumulation is driven by the following rules:
1. If the rate of profit is below the rate of interest then accumulation is reduced, in this case by 3%.
2. If the rate of profit is greater than the rate of interest then accumulation grows by 6% relative to last years rate of accumulation.
3. If as a result of rule 2, the total employed workforce would be greater than the available labour force, then realized accumulation is constrained to be no more than would achieve full employment.
We assume that the interest rate is regulated by a central bank which attempts to stabilize employment levels. If employment approaches 100% it will raise interest rates, but if unemployment rises too high, the bank attempts interest rate cuts.
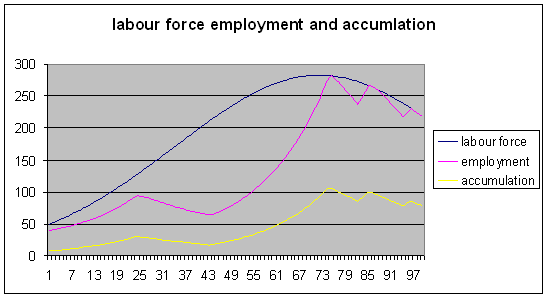
|Figure 6
Figure 6 plots the evolution of the population and of the employed population. The most striking feature is that in the initial 25 years the employed workforce rises rapidly, then accumulation suddenly falls off producing a consequent fall in employment. Looking at the evolution of profit and interest rates the reason for this becomes evident.
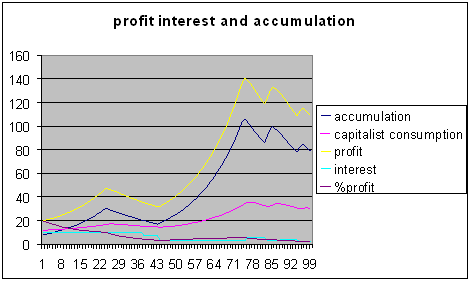
Figure 7
In year 25 because of the rise in the capital stock relative to the employed population, the rate of profit falls below the rate of interest. This produces a decline in accumulation. This in turn reduces the mass of profit as well as the rate of profit. The bank eventually responds by cutting interest rates sufficiently to restart accumulation. A long period of low interest rates allows accumulation to resume until labour shortages eventually force the bank to raise interest rates. During the last 30 years of the simulation the simulated economy oscillates between full employment and periods of recession. During this period the trend of both rates of profit and real interest rates is downwards.
We think that this is a reasonably realistic portrait of what tends to happen to a closed capitalist economy in the long run. Obviously actual economies are not closed so that accumulation can rise higher than could be supported by the domestic workforce. Similarly, an individual economy may offset a decline in the labour force by immigration. However if we consider the global economy, this sort of mechanism could operate, provided that there were some international coordination of interest rates.
Conditions of accumulation
If there is a conflict between what the macro-economic equations tell us and the conclusions of Roemer’s microeconomic argument, then one of the arguments must be wrong. Either :
● One of us has a logical flaw in our deductive arguments.
or
● The initial assumptions made in one or other of the arguments are incompatible.
Let us allow, for now, that each argument is logically well founded and follows from its initial premises. Roemer’s argument has shown that capitalists will not carry out investments in new production technologies if the result of these would reduce the average profit rate in the whole economy, and we show that any net accumulation greater than the rate of growth of the working population will tend to reduce profit rates in the long run.
One conclusion from this might be that there will never be any accumulation faster than the rate of population growth. It is possible that the micro-economics sets limits to the maximal rate of accumulation that macro-economy can exhibit. Another possibility is that some of Roemer’s micro-assumptions are invalid and should be dropped. In the end, as with all scientific hypotheses, the criterion has to be their ability to predict what actually happens.
We believe that there is evidence that over periods of decades in individual economies the rate of accumulation has exceeded the rate of population growth and that as a consequence the organic composition of capital has risen (Cockshott., Cottrell, and Michaelson, 1995), (Edvinsson 2003) []. Since this should not occur on the basis of the micro-economic arguments put forward by Roemer, this pre-disposes us to believe that there must be some premises in his argument that are not an accurate reflection of the way capitalist economies actually work.
Assumption of profit equalisation
Although Roemer’s argument is intended to provide micro-economic foundations for a discussion of the falling rate of profit it is not micro-economic in the neo-classical sense. Instead the micro-foundations are laid upon what amounts to a macro economic bedrock in the form of input output analysis. The prices and profit rates that firms are supposed to be responding are deduced as the solution to a set of linear i/o equations applying to the whole economy. There is obviously a fairly long tradition of Marxist economists analysing capitalist economies this way, most obviously in Sraffa ( 1960) and others such as Samuelson (1973) and Steedman(1981). The price theory that results is macro economic in the sense that its solutions depend upon knowledge of input output relationships across the whole economy. It also makes certain very strong assumptions about profit rates. It assumes that the rate of profit is the same for all industries and that it is independent of the organic compositions of capital in these industries. The existence of a tendency for profit rates to equalise across different industries was recognised by the classical economists and by Marx, and it was the attempt to reconcile this tendency with the labour theory of value that gave rise to the famous transformation problem; however, an assumption of fully equalised profit rates in all industries is neither realistic nor appropriate when the problem under consideration is the time evolution of profit rates.
Capitalist economies are inherently chaotic and one would therefore expect an equilibrium condition to be characterised not by a single profit rate, but by a stable probability density function describing the distribution of profit rates. This observation is due to Farjoun and Machover (1983). This spread of profit rates will occur both within individual industries and accross sectors of the economy. This spread of profit rates turns out moreover not to be simply random. Emprical data indicates a systematic inverse relationship between organic composition of capital in an industry and the mean rate of return on capital in that industry (Cockshott and Cottrell (2003). We will argue below that the presence of such a distribution of profit rates undermines the arguments that Roemer deploys against a tendancy for the rate of profit to fall.
Even in the absence of such empirical data, the assumption of equal equilibrium profit rates in an industry is inherently implausible in the context of a discussion of the effects of technical change. The process by which equilibration of profit rates is supposed to come about was originally invoked by Ricardo in the context of comparing things like wine maturation and forestry which had multiple year turnover times, with corn growing which had an annual turnover period. The argument was that capital would only be invested in low turnover activities if it yielded the same return as in normal agriculture. Whilst this argument may have some plausibility when applied to activities agriculture and viticulture where the rate of technical change is low, and decades or centuries can be allowed for the establishment of relative prices it is less clear that it can be invoked where there is rapid technical change. In this case the time taken to establish equilibrium could be much longer than the lifespan of the technology. This is especially true in some industries with a high capital/labour ratio, ones which are particularly relevant to the question at hand. Consider the Victorian railway booms. Here was an entirely new technology requiring huge capital investment. The lifetime of the capital in the form of bridges embankments and stations would be a century or more. The booms resulted in over capacity, which, by the early 20th century resulted in a process of line closures. But before the capital invested in railways could depreciate to a level at which the return of railway capital reached equilibrium levels, the whole technology was superseded by road transport. The sort of equilibrium that Roemer invokes in his arguments can be so long in coming that the industry has died before it is relevant. Keynes’s aphorism was no joke.
Fixed type structure of output vector
This points to another limit to what Roemer and Okishio have demonstrated. Their arguments have addressed technical change in the context of a pre-existing set of products. They consider which technologies will be chosen to reduce costs in an existing industry. This says nothing about what happens when new products are invented. Consider the shift from horse vehicles to petrol cars. Even if one grants that the Okishio theorem pointed to a restraint on the organic composition of capital in the manufacture of horse drawn carts, this would place no limitation on the organic composition of capital in the manufacture of lorries. In the semi-conductor industry, successive generations of chips are different products. They have new capabilities and their physical construction is different. Typically each generation has smaller transistors. To produce the smaller transistors has required successive fabrication plants to be able to produce images with shorter and shorter wavelengths of light, moving from visible light to far ultraviolet.
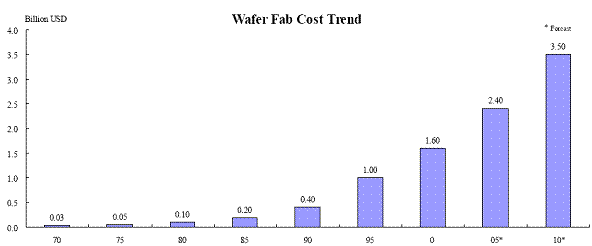
Figure 8. Rise in wafer fab costs, ( IC Insights, 2002)
This process has driven the costs of fab plants up. There is another aspect to the question of economic limits. Rock’s Law (Ross 2003) states that the capital requirements rise exponentially along with chip densities. The cost of a new semiconductor fabrication plant in 1966 was US $14 million. In 1995, the typical cost of such a plant had risen to US $1500 million. The current cost of a modern fabrication plant is now approaching US $10 billion. These changes have occurred as production moves to successive generations of processor chip. Since each generation is a new product, the Okishio theorem gives us no purchase on what is happening. The example is taken from one of today’s leading industries, but the same process is occurs more generally. Advances in science make sophisticated products possible. Such products often involve substantial investment in new fabrication technologies, research, prototyping etc, without which the product itself would be impossible. All of these constitute possible avenues for the absorption of new capital investment which can raise the organic composition of capital in society as a whole.
Extended or simple reproduction
At one level the sort of analysis involved in the Okishio theorem is macro-economic, in that it considers the input/output matrix of the economy as a whole. But in another sense it abstracts away from some crucial details of the input/output structure. All that is used in the analysis is the technical coefficient matrix of the economy. The actual destination of the net output is not analysed in detail. We know from the technical coefficient matrix how much of gross output will be consumed as means of production in the current period, and we know from the real wage vector how much of the remaining net output will be consumed by the working class. But the analysis leaves undefined the composition of the surplus product vector.
No explicit assumptions are made that the system is in a steady state of simple reproduction, so the analysis applies to growing economies. For a growth path with equilibrium profit rates to be followed,
1. the firms producing new means of production must produce exactly the right amount of each product;
2. other firms must place new investment orders for exactly these products;
3. the capitalist class as a whole must chose to spend sufficient on unproductive consumption to exactly absorb the rest of the surplus product.
Were the total orders for investment goods and luxury consumption to fall below the level needed to fully monetise the total surplus product, then the actual rate of profit would fall short of the equilibrium rate of profit given by Roemer’s linear equation model. The whole scenario of growth along an equilibrium growth path, is quite counter to what we know of the history of capitalism, which has always been characterised by an economic cycle. In these cycles the level of investments and profit rates fluctuate. Steady growth along a von Neumann ray, is, if anything, an idealised presentation of the behaviour of a centrally planned rather than a market economy. Even if a real capitalist economy could momentarily achieve the uniform equilibrium rate of profit hypothesised in Roemer’s formalism, this state would be unstable. The first investment slowdown would depress profits in means of production industries relative to others. Soon you would be back to quotidean reality with a dispersion of profit rates between industries, and between firms in individual industries.
If we drop the unrealistic assumption of there being a single profit rate which coincides with the average rate of profit, what are the implications for Roemer’s argument?
The key point is that the rate of profit no longer appears as a given or datum to be used in calculations by individual capitalists. Insofar as an average rate of profit exists, it can only be discovered by analysis of national income statistics, it is not something immediately present to capitalist calculation. Thus decisions on what is a rational discount rate to utilise in planning future investment can not be based on the average rate of profit.
What is present as a given datum is the rate of interest on loan capital. The rate of interest is something quite distinct from the average rate of profit, and is set by different mechanisms. While the average rate of profit in the economy can be plausibly deduced from considerations about aggregate production functions, the real wage and stocks of means of production, the interest rate is driven by monetary considerations including central bank policy.
On very general grounds we can expect the rate of interest to be below the average rate of profit for a substantial part of the business cycle. When this condition does not hold, a significant proportion of firms will be earning insufficient profit to meet their interest payment and would be threatened with insolvency. At any given time there are always some firms in this situation, but when the rate of interest rises above the rate of profit then a large fraction of all firms become insolvent. Since, under normal trading conditions, only a relatively small fraction of firms are insolvent, it follows that for most of the time interest rates are below average profits. From this it follows that it would be rational for most firms to engage in investments even if the rate of return on these investments was lower than they were currently obtaining - provided that the return was higher than they could get by depositing their cash in the banks. If the discount rate used in evaluating the future profitability of fixed capital is systematically lower than the current profit rate, then there can exist a pressure to raise the organic composition of capital, with a resulting depression of the rate of profit. Of course firms can never tell what profit they will actually obtain from investments, but Roemer’s arguments are based on firms taking current prices as given and projecting these into the future. He argues that they will not invest in fixed capital if, given current prices, the discounted rate of return on the investment would be less than the current rate of profit. This is what he terms a viable investment. He then shows that such viable investments can not depress the aggregate rate of profit. If firms actually use the rate of interest as the discount rate, then investments which on Roemer’s calculus are unviable and which tend to depress the average rate of profit, will in fact be undertaken.
It could be argued that the average rate of profit is actually available to firms in the form of the rate of return on equities. We accept that there will be feedback relations between the rate of return on equities and the rate of return on real capital. If an individual firm has a high rate of return on real capital invested, its equity price is likely to rise to reflect this. If we furthe assume that arbitrage operations on the stock market will tend to narrow the dispersion of rates of return on equities, then a rise in the average rate of profit, will tend, other things being equal, to increasse the average rate of return on equities. But for the purposes of looking at the overall trajectory of profit rates, we can not assume that the real rate of profit is the only factor determining the return on equities.
Suppose that we have the following situation:
1. a static working population;
2. a rate of return on equities equal to the general rate of profit.
By the extended version of the Okishio theorem covering fixed capital, then if we have an equilibrium rate of profit there will be no viable net investment in fixed capital. Any such investment would raise the organic composition of capital and is hence excluded. This implies that there should be zero net issue of new equities. If the rentier class as a whole decides to make no net saving, then the situation is stable. But this is unlikely. If the rentiers attempt to accumulate capital by investing in shares, the net effect will be to bid up the price of equities, given that no new equities are being issued. The effect of this is to depress the rate of return on equities. This will affect the discount rate used in assesing investment projects. Previously unprofitable ones will seem profitable. New equities will be issued and the proceeds invested. Given that the population is static, this will raise the organic composition of capital and depress the real rate of profit.
The weakness in Roemer’s argument stems from a fundamental
failing of the entire price of production
The mechanism required to equilibrate the return on equities is quite different from that posited by the Sraffian school to create an equal rate of return on real capital. Equity returns can be equilibrated by simply marking their prices up or down. The rate of return on invested capital in different industries can only be brought into equilibrium by real capital flows between industries. If steel production earns a lower rate of profit than natural gas extraction, then in order to equilibrate the two, capital has to be withdrawn from steel production and switched to gas drilling. This has to continue until resultant shortages of steel force steel prices up and surpluses of gas push down gas prices. The speed with which this adjustment can occur will be constrained by the depreciation rate of fixed capital in the steel industry and the time taken to explore, discover and bring on-line new gas fields. It is evident that this process must be much slower than the equilibrating processes in the equity market. So we would expect a relatively wide dispersion of profit rates on the real side and a narrow dispersion of profit rates on the equity side.
Insofar as firms have an indication of the general rate of return on capital, it comes through the intermediation of the stock market. But overall levels of equity prices like the Dow-Jones and FTSE indices are affected by factors other than the rate of return on real capital.
1. Their traces contain broad spectrum noise. This noisy character will alone ensure that for much of the time the apparent rate of profit is lower than the real rate of profit anticipated by companies making investment decisions.
2. The overall price of equities will be influenced inversely by the prevailing rate of interest. This in turn is influenced by state monetary policy and ultimately by political as well as economic considerations. Political pressures to keep interest rates low can make capital ‘cheaper’, undermining the relationship between the real rate of return and investment decisions.
3. The level of savings, by companies, rentiers and wage earners can influence stock market conditions, raising or depressing the benchmark rate of return.
For these reasons we consider Roemer’s theoretical demonstration that investment decisions bounded by the real rate of profit can not lead to falls in the general rate of profit to be inapplicable to the real world.
Implications of falling profit rates
As capitalist economies mature they undergo demographic transitions with birthrates tending to fall below the reproduction level. This presages a period of stagnant or declining labour forces. This can only be partially offset by raising the retirement age, increased female participation in the labour force etc. Under these circumstances any net capital accumulation will tend to depress profit rates. Does this matter?
What are the implications of a long term decline in profitability?
One
possibility is that is does not matter. If interest rates also undergo a long
term decline so that they remain below average profit rates, then accumulation
and economic activity could be maintained. Suppose, however, that there exists
some fixed risk premium between interest rates and industrial profits. Let us
suppose that unless interest rates are 3% below anticipated profits firms will
not invest. It follows that if the real rate of profit falls below 3%, there
will be no positive interest rate compatible with continued accumulation. Such
a configuration would imply a future of stagnating accumulation reminiscent of
the recent experience of
In an economy in which pension provision is privately provided the prospect of falling rates of return on investment has other implications. Lower returns on equities would imply that individuals would have to build up larger investments to provide for retirement. Whether this occurs voluntarily or by the state mandating higher contributions to pension schemes, the net effect is likely to aggravate the problem of falling returns. High savings ratios will depress demand and thereby reduce investment opportunities in the consumer goods industries. The inflow of additional savings will also tend to bid up equity prices further reducing the rate of return, which will have feedback effects on the viability of pension schemes.
A falling return on capital has other social implications. The amount of capital required to yield an income for one person will rise. This would constitute a barrier to entry into the employing class, so upward class mobility would be restricted.
These
effects can be offset by international mobility of capital and labour. On a world scale, population is rising as is the
capitalistically employed population. To the extent that capital can flow to
this population, or the people can migrate, then the average international rate
of profit need not decline.
We have argued that returns on capital should be understood in the context of accumulation, population dynamics and the process of expansion of capitalism at the expense of other forms of economy. A focus purely on technical change as the controlling factor of profit rates can give misleading results. When the broader view is taken, we consider that declines in profitability are likely to be a problem for the global economy in the 21st century.
Cockshott, W. P. and A. Cottrell, 2003, ‘A note on the organic composition of capital and profit rates’, Cambridge Journal of Economics, vol 21, pp 545-549
Cockshott, W. P., A. Cottrell, and G. Michaelson,
1995, ‘Testing Marx: Some New Results from
Edvinsson,R., A Tendancy
For the Rate of Profit to Fall, Paper presented at the economic-historical
meeting in
Farjoun, E., Machover, M., The laws of chaos, Verso, 1983.
Ross, P.E. 5 Commandments [technology laws and rules of thumb] , Spectrum, IEEE, Volume: 40, Issue: 12, pp 30- 35,2003.
Samuelson, P. A.. Reply on marxian matters. Journal of Economic Literature, 11:64-68, 1973.
Steedman, I, . Marx after Sraffa.
Verso,
Sraffa, P. 1960. Production of Commodities by Means of
Commodities,