1. INTRODUCTION
|
Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on the first page. To copy otherwise, or republish, to post on servers or to redistribute to lists, requires prior specific permission and/or a fee.
Conference proceedings ISBN 80-86943-03-8 WSCG’2006, January 30-February 3, 2006 Plzen, Czech Republic . Copyright UNION Agency – Science Press |
Filmmakers today are increasingly turning towards an all-digital solution, from image capture to post-production and projection. Due to its fairly recent apparition, the digital cinema chain still suffers from several limitations which can hamper the productivity and creativity of cinematographers and production companies.
1.1 Data Compression
The current standard for the storage and transfer of film data is the CINEON or DPX format (Digital Picture eXchange). Each DPX file encodes an individual frame as an array of uncompressed pixel values. Such files are extremely large, at typically over 10MB per frame, which corresponds to over a Terabyte per hour of film at 24 frames/second. Despite the ongoing technological advances in disk capacity and network speed, this makes the storage and transfer of movie data between collaborators along the digital cinema chain impractical and costly.
In order to reduce the amount of data necessary to encode a movie sequence, it is necessary to use some form of compression. Traditional video compression methods such as MPEG cannot be used within the context of digital cinema as they result in visual artifacts such as ringing which degrade image quality: such compression is termed lossy. Lossless compression methods, on the other hand, preserve the integrity of the signal, however the reduction in data they offer is minimal.
1.2 Spatio-Temporal Resolution
The variety of means by which digital material can be obtained (e.g., 35mm film scans, high-definition film cameras, video cameras) and the various display methods (TV, HDTV, projection) have led to the coexistence of multiple resolution standards, such as: PAL (720x576 pixels), 1080i (1920x1080 pixels), 2K (2048x1080 pixels) and more recently 4K (4096x2160 pixels). Similarly, this also occurs in the temporal domain, where values of 24, 30 or 60 frames/second coexist. This absence of a unified standard of spatial and temporal resolution implies that digital film material from different sources is more difficult to combine and composite at the production stage.
1.3 Aim of this Work
In the light of these issues, it is clear that a novel approach to the encoding of movie sequences is needed that will meet the requirements of the movie industry.
Firstly, in order to minimize the amount of data necessary to encode a sequence whilst maintaining high standards of image quality, we propose that a suitable approach should allow for perceptually lossless compression i.e., the artifacts introduced by the compression process should be constrained to verify a chosen perceptually-based criterion. The work presented here proposes that the local properties of the compressed image should remain within the statistical bounds of intrinsic camera noise..
Secondly, the multiplicity of resolution standards is inherent to the discrete nature of the pixel representation: digital film is divided into a finite number of frames; frames are composed of a finite number of scanlines which in turn are made of a finite number of pixels. In reality, physical objects exhibit a continuous nature (at least at the macroscopic scale) in both spatial and temporal domains. Although this essential quality is lost in the digitization process, it is possible to approximate the original continuous signal by using analytical functions to interpolate the discrete data. A signal encoded in such a way can be evaluated at any arbitrary spatio-temporal resolution and, as a result, movie sequences expressed in this form are no longer tied to their native resolutions and can therefore be easily composited together.
This paper proposes to define the basis for a resolution-independent image representation that allows perceptually lossless, distortion-constrained compression. The next section examines previous approaches in image compression and image encoding. Section 3 presents an algorithm for distortion-constrained movie compression. Section 4 details the polynomial encoding method used here, and Section 5 examines possible quantization schemes. Preliminary results are shown in Section 6.
2. EXISTING WORK
The increasing popularity in digital video has lead to a wealth of research into the encoding of moving images. The following approaches are the basis for the most widely used video codecs.
2.1 3D-Discrete Cosine Transform
By applying a 3D Discrete Cosine Transform to image sequence blocks and quantizing the resulting coefficients in an appropriate manner it is possible to achieve high compression ratios [Wat01a]. The main disadvantages of this approach are the blocking artifacts that appear at high compression rates, the ringing artifacts and occasional blurring that appear at sharp edges. Most of the current video codecs (MPEG-1,-2,-4, H.26x) are 3D-DCT based.
2.2 3D-Discrete Wavelet Transform
The 3D Discrete Wavelet transform (3D-DWT) works by decomposing an image sequence into frequency sub-bands [Wan93a]. Most wavelet-based algorithms achieve compression ratios similar to those obtained with DCT-based methods yet do not exhibit blocking artifacts. The overall visual quality is usually superior (both perceptually and in terms of PSNR) to DCT-based methods. Unfortunately, wavelet-based algorithms also suffer from blurring and ringing artifacts at sharp edges. The 3D-DWT is used in a few codecs, such as Intel Indeo 5.x.
2.3 Vector Quantization
Vector Quantization works by examining similarities in local image structure [Lin80a]. Although the VQ encoding method is computationally expensive, the decoding itself is very fast. Unfortunately, this method also suffers from blocking artifacts at higher bit rates. VQ can be applied in conjunction with 3D DWT [Yao92a]. Vector Quantization is used by codecs such as Cinepak and Indeo 3.2.
2.4 Polynomial Fitting
By fitting polynomial functions to 3D pixel blocks at different spatial scales it is possible to encode image sequences accurately within a given amount of error. By combining this scheme with scalar quantization methods it is possible to achieve high compression ratios [Cyg96a] without suffering from the ringing artifacts found in other methods.
The work presented in this paper uses polynomial-based encoding as it has been shown to offer compression without resulting in ringing artifacts. Additionally, polynomial functions make up a suitable analytical basis for a resolution-independent representation.
3. A GENERIC ARCHITECTURE FOR ENCODING DIGITAL MOVING IMAGES
In this section we will present a generic architecture for distortion constrained compression of digital cine material. The architecture allows a variety of implementations all sharing the same basic approach. The following concepts are the key to the architecture:
1. The cine sequence is treated as a three dimensional array of samples handled by voxel compression techniques.
2. In all cases a scale space approach analogous to image pyramids is used to capture correlations accross voxels in time and space.
3. A closed loop feedback system is used to compensate for artefacts introduced by quantisation at higher levels.
4. The quantisation schemes used are tailored to constrain errors to be within the bounds set by shot noise.
|
|
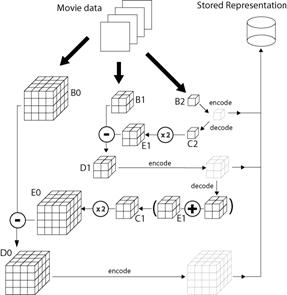
Figure 1. Encoding Architecture
The first phase of the algorithm, illustrated in Figure 2.1, gathers individual digital frames into three dimensional blocks of pixels. Preferably this partitioning into blocks should occur at 'cuts' or shot boundaries, but this is not essential. The Figure shows the processing of one such block, labeled B0.
The blocks are then spatially and temporally filtered and downsampled to form a pyramid of such blocks each of which is smaller in each dimension by a scale factor or where r is typically 2 or 3. These blocks are labeled B1, B2 in Figure 2.1, but the number of such block levels need not be restricted to 3 as shown. We shall refer to this sequence of blocks as a pyramid by analogy with the commonly used image pyramids of Burt etc. We refer to the largest block as being at the base of the pyramid and the smallest as being at the top.
Consider the top block, B2 in the case of Figure 2.1. We apply to it, some encoder, which in the case of the top block may be null. A copy of the encoded representation is sent to the output stream after which the encoded representation is internally decoded by the compressor and stored in block C2.
C2:= decode(encode(B2))
An interpolation algorithm, which may exploit features of the encoding previously applied, is then used to expand C2 by a scale factor of to obtain block E1 which is the same size as block B1 but lacks high frequency information.
E1:=expandby(r,C2)
E1 may include some artifacts due to quantisation or the interpolation technique used. We then form
D1:= B1-E1
so that D1 is a differential block containing the information from B1 that was not captured by the encoding of E1.
D1 is then itself encoded, perhaps using a different encoder than that used at the top level. The encoded output is appended to that produced for the top level of the pyramid. Again the encoded form of the current level is internally decoded and added to E1 to produce C1.
C1:= E1 + decode(encode(D1))
The block C1 should now be a close approximation to the original downsampled block B1. It can be expanded again by a factor of r to form a block E0, as large as the original source block B0. Subtracting them we again obtain a difference block:
E0:=expandby(r,C1)
D0:=B0-E0
which we encode, appending the ecoding to the output stream.
This generic architecture can clearly accept a number of different encoder functions, see the earlier work of Burt [Bur83a], Tao [Tao05a] etc. We propose to explore the use of encoders based either on polynomial approximations or on vector quantization. The encoders used must all be constrained to work within the limits of shot noise.
It might seem that since all the errors from higher levels will be concentrated in the block E0, the quality of the encoding at higher levels is not critical. When considering the quality of the final output this is true, however when considering the efficiency of encoding it becomes worth constraining the quality of encoding at higher levels. A quantization error affecting one pixel at level n in the pyramid will affect pixels at level n-1 and will presumably require more encoded bits to correct at level n-1. The exception is when the error that would be generated for the pixels at level n-1 are less than the shot noise level and can thus be discarded. In this case a coarser quantization at level n saves bits at both level n and level n-1.
4. POLYNOMIAL ENCODING
4.1 Polynomial Fitting
This section describes a polynomial-based encoding scheme for the 2D case (single frame). Its extension to the 3D case (mulitple frames) is not detailed here for the sake of simplicity but can be easily derived from the 2D case.
Given a set of N image pixels it is possible to find a bivariate polynomial surface P with N coefficients which passes exactly through all N points by solving a linear system of N equations. We consider a set of 9 pixels arranged on a 3×3 rectangular grid. The polynomial P which interpolates the pixel values can be defined as :

where a,b,c,d,e,f,g,h,k are the polynomial coefficients.
For a 3×3 sub-image defined over the coordinate set {-1,0,1}×{-1,0,1},
it can be shown that the polynomial coefficients can be computed by convolving
the sub-image with kernels corresponding to derivation operators expressed as
finite difference scheme over the {-1,0,1}×{-1,0,1}domain. For example, the kernel for
the xy coefficient corresponds to the ![]() operator expressed as a set of
finite differences. Once all coefficients are computed, it is possible to
compute the image value at any subpixel location by evaluating the polynomial
for the corresponding values of x and y. The original image can be obtained by
rendering each 3 by 3 pixel block Bij
from the corresponding coefficients as follows:
operator expressed as a set of
finite differences. Once all coefficients are computed, it is possible to
compute the image value at any subpixel location by evaluating the polynomial
for the corresponding values of x and y. The original image can be obtained by
rendering each 3 by 3 pixel block Bij
from the corresponding coefficients as follows: 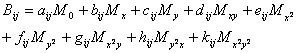 where
where ![]() are the polynomial coefficients for
the block located at row i and column j and the M are the
corresponding 3x3 masks e.g.,
are the polynomial coefficients for
the block located at row i and column j and the M are the
corresponding 3x3 masks e.g., ![]() over the {-1,0,1}×{-1,0,1}domain.
over the {-1,0,1}×{-1,0,1}domain.
4.2 Error Bounds on Polynomials
The polynomial obtained by the method described in the previous section describes the corresponding 3 by 3 pixel subimage with total accuracy. With 9 polynomial coefficients used to encode 9 pixels, this method does not present any advantage in terms of compression so far. One way to achieve compression is to apply some compression algorithm to the polynomial coefficients. In the case of lossy compression, the original coefficient values will not be preserved and the accuracy of the polynomial fit will be lessened. However, it is important to be able to verify that the resulting fitting error remains within the bounds defined by the Poisson criterion. This section details a method to evaluate the fitting error caused by perturbing the polynomial coefficients.
4.2.1 Mean Squared Error
Let da, db, ..., dk be the perturbations added respectively to polynomial coefficients a,b, ..., k. The corresponding polynomial Pd is:
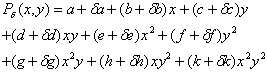
By developing this expression it can be shown that the mean squared fitting error over the 3 by 3 subimage due to these perturbations is given by the following quadratic form:
![]()
where D is the vector containing the perturbations da, db, ...,dk and W is a square matrix containing the products xmyn summed over the {-1,0,1}×{-1,0,1} range (0 < m,n < 5). By construction W is a symmetric matrix.
4.2.2 Variance of the error
The variance can be derived from the expression of the mean squared error by using the formula:
![]()
where e2 is the mean squared error as described in the previous section, and m2 is the square of the mean of the error values. m can be obtained with the following expression:
![]()
Being able to compute the statistical moments of the signal analytically from the perturbation applied to the polynomial coefficients allows us to easily verify whether applying compression to a polynomial breaks the chosen criteria for perceptually lossless compression.
5. QUANTIZATION SCHEMES
Our basic method of encoding up to now is entirely lossless. The polynomials are estimated with the number of coefficients equal to the number of data points, allowing lossless representation of the original data, provided that the coefficients are stored to sufficient numeric precision.
The format only becomes a compressive one if we are able to
- Represent the coeffiecients with fewer bits than in the original representation;
- Discover redundancies that allow entropy coding.
This section will deal with quantisation techniques that economize on the number of bits used to encode the coefficients. Section 5 will cover entropy encoding techniques.
5.1 Quantization
Quantization is the term given for the use of a finite set of exemplars to approximate real valued scalars or vectors.
The data we want to represent are a block of polynomial coefficients. The numbers in this block will not be real valued, but will be held initially to some finite precision. If B is a block of such coefficients and we have two functions E( ) which encodes the coefficients and a function D( ) which decodes them, we require that:
![]()
where ![]() is a metric on the coefficient
space and
is a metric on the coefficient
space and ![]() is an error threshold chosen to be
within the expected level of shot noise. We wish in addition that:
is an error threshold chosen to be
within the expected level of shot noise. We wish in addition that:
![]()
where l( ) is the length function returning the number of bits encoding B or its encoded representation.
5.2 Vector versus Scalar
There are two general approaches that can be taken to
quantising such data. The simplest approach would be to encode each of the
coefficients ![]() individually as a code
individually as a code ![]() with
with ![]() . This
process is shown diagrammatically in figure 2.
. This
process is shown diagrammatically in figure 2.
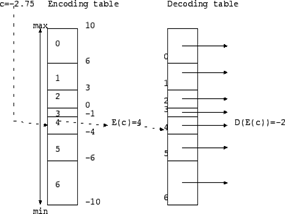
Figure 2. Encode and Decode tables used for scalar quantization
If one starts off with coefficients stored as floating point numbers, then the encoding table can be searched in logarithmic time using a binary search. If one starts out with coefficients stored as fixed point numbers to some modest precision the encoding table can be implemented as a simple array lookup indexed on the coefficient.
Note that the encoding table does not need to use equally sized bins. Ranges whose values occur infrequently can be approximated using larger bins, those with frequently occurring values can use smaller bins. There will be a trade-off between larger bin size - which increases the quantization error, and frequency of occurrence. A low frequency of occurrence reduces the probability that the quantization error associated with the bin will occur.
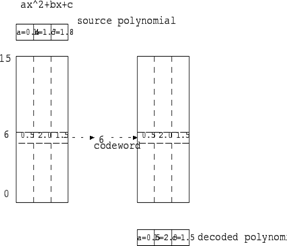
Figure 3. Encoding and Decoding processes using vector quantization
In this case we use the same table for both the encode and decode process and at least in principle, perform an exhaustive search during encoding. In practice there exist algorithms that allow a faster lookup of the encoding table.
This scalar quantization approach results in one code value per coefficient in the polynomial. An alternative approach is to approximate the whole block of polynomial coefficients with a single codeword as shown in Figure 3. This is vector quantization.
The advantage of vector quantization is that it achieves significantly higher compression than scalar quantization. The disadvantage lies in its poor performance on high temporal and spatial frequencies.
For vector quantization it is probably more efficient to use pixel values rather than polynomial coefficients when performing a search of the quantization tables for the best match. Use of pixel values slightly simplifies the computation of the error metric to be used in finding the best matching vector in the tables. If pixel vectors are used for lookup, then one can follow a Euclidean metric and simply minimize the mean squared error between codebook entries and the vector for which a match is being sought, thus:
![]()
Where ![]() is the ith pixel of the bock, and
is the ith pixel of the bock, and ![]() is the
ith parameter of the jth table entry. If one uses polynomial coefficients, then
as explained in section 4.2, coefficients
contribute differing amounts to the final error. This can be compensated for by
an appropriate weighting vector:
is the
ith parameter of the jth table entry. If one uses polynomial coefficients, then
as explained in section 4.2, coefficients
contribute differing amounts to the final error. This can be compensated for by
an appropriate weighting vector:
![]()
where ![]() is the ith coefficient of the
polynomial, the table now stores polynomial coefficients and
is the ith coefficient of the
polynomial, the table now stores polynomial coefficients and ![]() is the
ith element of a weight vector. This requires an extra m+1 multiplications per
comparison, which represents about an extra 30% more instructions in the inner
loop of the comparison. It is a matter of judgment whether this is acceptable.
is the
ith element of a weight vector. This requires an extra m+1 multiplications per
comparison, which represents about an extra 30% more instructions in the inner
loop of the comparison. It is a matter of judgment whether this is acceptable.
5.3 Quantizer Design
It is intended that the encoder will use the following algorithm to perform quantization:
- Perform VQ encoding on a block, and append this to the representation.
- Estimate the error that will ensue. If the error is below the shot noise, then the quantization algorithm terminates at this point.
- Estimate the coefficients of the polynomial ( if that was not done in a previous step )
- Form the difference between the true polynomial coefficients and those given by the vector quantizer.
- Perform scalar quantization on the difference values of the coefficients and append the quantized results to the representation.
5.4 Context Sensitivity and Noise
The quantization tables, whether for scalar or vector
quantization should be sensitive to the mean brightness of the locality in
which they apply. The local in-camera shot noise level can be well approximated
as ![]() ,
where
,
where ![]() is
the mean brightness obtained from higher pyramid levels. If the quantization
process is to be within the shot noise, this implies that the quantization
table used to encode differential information must be a function of the mean
brightness of the locality. The quantization bands used in the table should be
chosen so that the bands are no wider than the shot noise in this locality -
and that shot noise can itself be obtained as a function of information
supplied by higher pyramid layers.
is
the mean brightness obtained from higher pyramid levels. If the quantization
process is to be within the shot noise, this implies that the quantization
table used to encode differential information must be a function of the mean
brightness of the locality. The quantization bands used in the table should be
chosen so that the bands are no wider than the shot noise in this locality -
and that shot noise can itself be obtained as a function of information
supplied by higher pyramid layers.
This implies a two dimensional encoding table, indexed successively by the estimated shot noise level and by the differential value to be encoded.
The scalar quantization tables can be constructed using the following algorithm:
- A histogram H of the frequency of occurrence of each differential input code. This histogram is assumed to have been computed by statistical analysis of a large number of images.
- A specified shot noise level s
A scalar quantization tree usable to generate variable bit length codes to represent the quantized numbers.
- Analyze the histogram and find its mean.
- Store this mean value as the current node of the tree.
- Split it into two histograms
 about the mean
value.
about the mean
value. - Find the mean of each of the sub histograms.
- If the difference
between the means is less than the shot noise terminate recursion
otherwise, create new left and right sub-nodes and recurse applying steps 1 through 5 to each, having passed the
 to
the recursive applications.
to
the recursive applications.
The tree so constructed can be used to output variable length codes as follows:
function encode(t:tree; c:coefficient;var length,code:integer)
begin
if t<>nil then
begin
if t^.value<c then
begin
length:=length+1;
code:=code*2;
encode(t^.left,c,length,code);
end
else
begin
length:=length+1;
code:=code*2+1;
encode(t^.right,c,length,code);
end
end
end
6. PRELIMINARY RESULTS
The standard MPEG test sequence “foreman” was put though the resolution-independent representation, rendered at four times the framerate and rendered at twice the initial dimensions. Figures 4 and 5 contain images taken from the resulting sequences.
These results illustrate the capacity of our scheme to achieve a resolution-independent representation in both spatial and temporal domains. However, the benefits of such a representation are only valuable if the resulting images are of high enough quality. When rendered at the original framerate & resolution, the processed sequence was considered exactly identical to the input (the total squared error over 18 frames was less than 10-20 intensity steps – error only due to the limited precision of the computer). In the case of interpolated rendering, the images produced were visually pleasing.
Thorough examination reveals that, in the presence of high frequency information in the original sequence, the current interpolation method can sometimes overshoot and result in pixel values greater than 255 (or smaller than 0). These can result in small artifacts.
This issue is the focus of our current work and can be solved by establishing a greater continuity between adjacent polynomials in order to ensure a smooth interpolation. Further research will investigate the effect of different quantization methods on video quality and the compression ratios achievable by the algorithm. As our work to date has utilized monochrome imagery, determining the most appropriate color space to adopt for the new representation will also be a priority.
7. REFERENCES
[Bur83a] "The Laplacian Pyramid as a Compact Image Code", P.J. Burt, E.H. Adelson, IEEE Transactions on Communications, vol. 31, n. 4, 1983, pp 532-540
[Cyg96a] “3-D Block Decomposition Approach for Video Coding”, Boguslaw Cyganek, Image Processing & Communications, An International Journal, 1996, vol. 2, n. 4
[Lin80a] “An Algorithm for Vector Quantizer Design” Y. Linde, A. Buzo, et al., IEE Transactions on Communication, 1980, vol. 28, pp. 84-95
[Tao05a] “Distortion-Constrained Compression of Three-Dimensional CLSM Images Using Image Pyramid and Vector Quantization”, Y. Tao, PhD Thesis, University of Glasgow, 2005
[Wan93a] “Wavelet Transform Coding using NVIQ”, X. Wang and S. Panchanathan, Proc. of Visual Communications and Image Processing – SPIE, 1993, vol. 2094, pp. 999-1009
[Wat 01a] “The MPEG Handbook: MPEG-1, MPEG-2, MPEG-4”, J. Watkinson, 2001, Focal Press
[Yao92a] “Image Sequence Coding using adaptive Vector Quantization in Wavelet Transform Domain”, S. Yao and R. J .Clarke, Electronic Letters, 1992, Vol. 28, n. 17, pp. 1566-1568