Lab 2- Introduction to Matlab

Matlab is a commercial piece of software sold by MathWorks. We will go through the functionality of thelanguage and environment in class

By next week’s lab you should have implemented the neural network defined in this note, and experimented with the visualisation properties of matlab in order to better understand how a neural network can represent complex mappings. If you have time it will be worth trying to summarise your results (with graphical output) and answers in a short report (you could use Word or Latex, for example), which I can then give you feedback on (but this will not form part of your formally assessed work). This will familiarise you with the graphic output methods, and be good practice for future assignments which will require an assessed hand-in report.

In the lab – Introduction to MATLAB

You will probably not finish this lab in the time available, but at least make sure that you have started MATLAB, know how to use the documentation, and have understood the task before the lab is over. You can then finish it off in your own time.

MATLAB is found in /local/matlab/matlab5/bin. Documentation can be found in /local/matlab/matlab5. Once this has been added to your path variable, you should be able to start matlab by simply typing matlab. Use the help command, and the demos command to get an overview of what’s available. General background information about matlab, including tutorials, can be found at http://www.mathworks.com

Visualising model behaviour

Use the mesh or surf commands to visualise the response of your network subject to inputs throughout the input space. If we take a function such as we can view its response using code like:

xrange = [0:0.01:1];

[Xin,Yin] = meshgrid(xrange); Create the sample points on a grid

output = Xin.^2+Yin; The colon turns array into vector

surf(Xin,Yin, output);

Note that sometimes in matlab we want to have our data in vectors rather than arrays, so to convert the 101 x 101 matrices storing Xin & Yin above into matrix composed of two 10201 x 1 vectors we could use:

inputs = [Xin(:) Yin(:)];

and to convert back to a matrix we could use:

reshape(Xin(:),length(xrange),length(xrange));

Implementing a simple Neural network

We will start off with a simple single-unit perceptron, as discussed in last week’s tutorial, then piece these together into a multi-layer perceptron with multiple ‘neurons’.

Single-unit perceptron

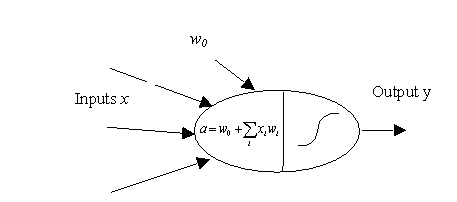
The mathematical model of a single neuron with a step-function response instead of the sigmoid is called a threshold unit. , where , so a is a linear function of the input vector. This is a useful starting point for understanding how neural nets can represent interesting models. w₀ is often called a bias connection, and is sometimes built into the w vector as a connection to an input which is always 1.

Implement this in Matlab, and view line and surface plots of the response for different settings of w and w₀, and for different ranges of input, in one and two-dimensional input spaces. Explain in words the effect of the w and w₀ parameters. Make sure that your implementation is simple – you should be able to implement the function in 1 or 2 lines of matlab, and it should be general (can be used for 100-dimensional input spaces without changing the code).

Give example neurons with weight vectors w and offsets w₀ which simulate AND, OR and NOT functions for two inputs. Is it possible to implement XOR? (Think of the truth tables supplying the test data, and ignore outputs for inputs other than 0 & 1.)

The mathematical model of a single neuron with a sigmoidal response is 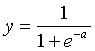, where . (Note that this is one of many possible models – piecewise linear functions, or other representations of sigmoid-like functions, such as tanh()). The w are the weight strengths (an n-dimensional vector, where n is the size of the input vector), and the x are the inputs. The sum of the excitation is represented by a, and the neuron’s output is y. Again, implement this in matlab and explain in words the effect of the w and w₀ parameters. Can you make the sigmoid look like a step-function just by changing the parameters? Make sure that your implementation is simple – you should be able to implement the function in 1 or 2 lines of matlab, and it should be general (can be used for 100-dimensional input spaces without changing the code).

Copy the dataset datalab1.mat from the course’s lab web-page http://www.dcs.gla.ac.uk/~rod/NC4/index.htm into your working directory and load it in to matlab (using load datalab1). The data provides a possible (artificially generated) sample of ballet dancers and rugby players, as shown in the figure:

Recreate this figure using the matlab plot commands. Can you combine the surface plots of your neuron outputs on the same graph as the data sets? If you want to convert a picture into .eps format for use with latex or Word, you can use print –depsc filename.eps

Try to set the parameters of the single neuron by hand to classify the data correctly. Is it possible? If you cannot separate the two classes completely, how would you decide which setting was least bad?

Multi-layer perceptron

A standard perceptron can be used to classify points which are linearly separable. If you can find a plane which will separate two classes of data they are linearly separable – how does this relate to the question about XOR above? If we want to solve problems which are not linearly separable, we must use more complex networks.

We are now going to see how easy it is to generalise the one-neuron case to a full network using Matlab.

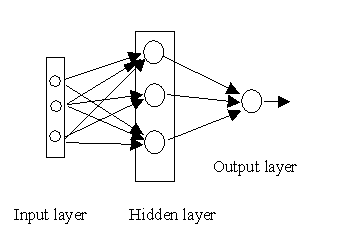
If we have an n-dimensional input layer, and an h-dimensional hidden layer, we can create a vector of activations using a command like a = w0 + x*w, where w0 is now an h x 1 vector, x is still an n x 1 vector, and w is now an n x h matrix. This can be passed to a sigmoid function as before, and the result of that can be used as an input to a further neuron.

Return to the dataset discussed earlier. Can you now separate the two classes with two or three neurons and a third layer, as implemented above? Can you explain in words what is happening in the different layers? Manual adjustment of parameters soon becomes tedious – next week we will implement a learning algorithm to do this for us!

Direct any queries or difficulties to me rod@dcs.gla.ac.uk - I’ll be pleased to help.

Roderick Murray-Smith