Contents

olymppoly.m

From A First Course in Machine Learning, Chapter 1. Simon Rogers, 31/10/11 [simon.rogers@glasgow.ac.uk]

clear all;close all;

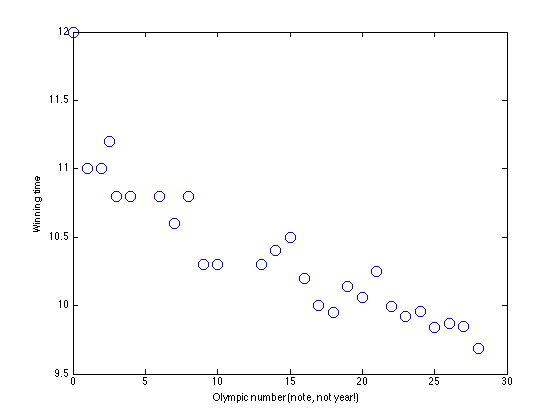
Load the Olympic data and extract the mens 100m data

load ../data/olympics.mat

x = male100(:,1);
t = male100(:,2);

% Rescale x for numerical reasons
x = x - x(1);
x = x./4;

% Plot the data
figure(1);hold off
plot(x,t,'bo','markersize',10);
xlabel('Olympic number (note, not year!)');
ylabel('Winning time');

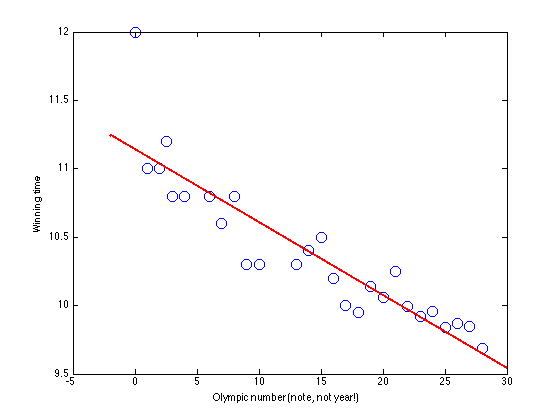
Linear model

plotx = [x(1)-2:0.01:x(end)+2]';
X = [];
plotX = [];
for k = 0:1
    X = [X x.^k];
    plotX = [plotX plotx.^k];
end

w = inv(X'*X)*X'*t;

% Plot the model
figure(1);hold off
figure(1);hold off
plot(x,t,'bo','markersize',10);
xlabel('Olympic number (note, not year!)');
ylabel('Winning time');
hold on
plot(plotx,plotX*w,'r','linewidth',2)

Quadratic model

plotx = [x(1)-2:0.01:x(end)+2]';
X = [];
plotX = [];
for k = 0:2
    X = [X x.^k];
    plotX = [plotX plotx.^k];
end

w = inv(X'*X)*X'*t;

% Plot the model
figure(1);hold off
figure(1);hold off
plot(x,t,'bo','markersize',10);
xlabel('Olympic number (note, not year!)');
ylabel('Winning time');
hold on
plot(plotx,plotX*w,'r','linewidth',2)

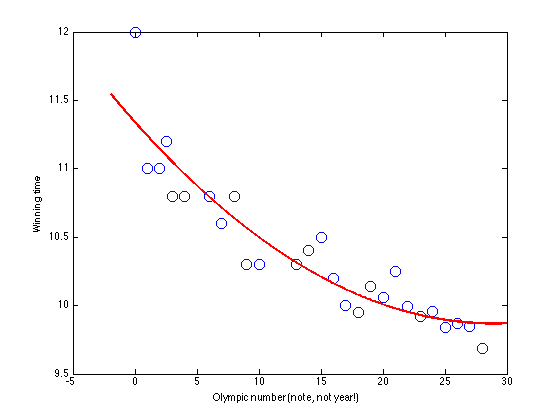
Quartic model

plotx = [x(1)-2:0.01:x(end)+2]';
X = [];
plotX = [];
for k = 0:4
    X = [X x.^k];
    plotX = [plotX plotx.^k];
end

w = inv(X'*X)*X'*t;

% Plot the model
figure(1);hold off
figure(1);hold off
plot(x,t,'bo','markersize',10);
xlabel('Olympic number (note, not year!)');
ylabel('Winning time');
hold on
plot(plotx,plotX*w,'r','linewidth',2)

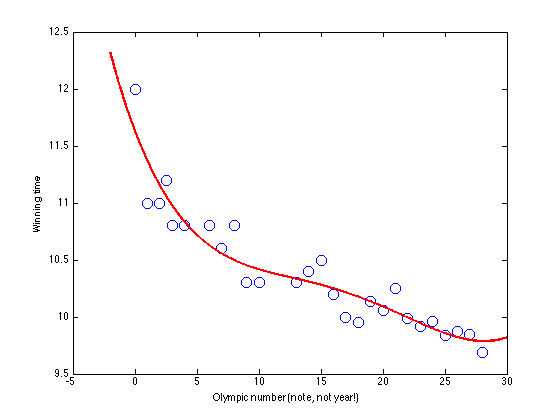
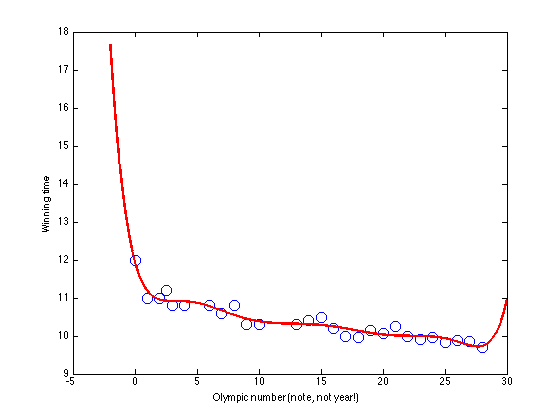
8th order model

plotx = [x(1)-2:0.01:x(end)+2]';
X = [];
plotX = [];
for k = 0:8
    X = [X x.^k];
    plotX = [plotX plotx.^k];
end

w = inv(X'*X)*X'*t;

% Plot the model
figure(1);hold off
figure(1);hold off
plot(x,t,'bo','markersize',10);
xlabel('Olympic number (note, not year!)');
ylabel('Winning time');
hold on
plot(plotx,plotX*w,'r','linewidth',2)

Warning: Matrix is close to singular or badly scaled.
         Results may be inaccurate. RCOND = 4.085559e-25. 

Published with MATLAB® 7.12