Contents

w_variation_demo.m

From A First Course in Machine Learning, Chapter 2. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] The bias in the estimate of the variance Generate lots of datasets and look at how the average fitted variance agrees with the theoretical value

clear all;close all;

Generate the datasets and fit the parameters

true_w = [-2;3];
Nsizes = [20:20:1000];
for j = 1:length(Nsizes)
    N = Nsizes(j); % Number of objects
    N_data = 10000; % Number of datasets
    x = rand(N,1);
    X = [x.^0 x.^1];
    noisevar = 0.5^2;
    for i = 1:N_data
        t = X*true_w + randn(N,1)*sqrt(noisevar);
        w = inv(X'*X)*X'*t;
        ss = (1/N)*(t'*t - t'*X*w);
        all_ss(j,i) = ss;
    end
end

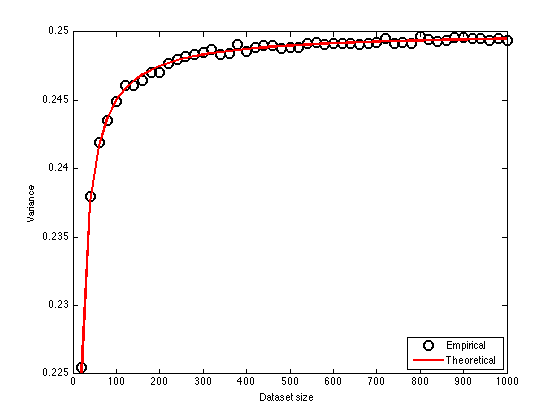
The expected value of the fitted variance is equal to:

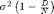$\sigma^2\left(1-\frac{D}{N}\right)$ where $D$ is the number of dimensions (2) and 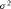$\sigma^2$ is the true variance. Plot the average empirical value of the variance against the theoretical expected value as the size of the datasets increases

figure(1);hold off
plot(Nsizes,mean(all_ss,2),'ko','markersize',10,'linewidth',2);
hold on
plot(Nsizes,noisevar*(1-2./Nsizes),'r','linewidth',2);
legend('Empirical','Theoretical','location','Southeast');
xlabel('Dataset size');
ylabel('Variance');


Published with MATLAB® 7.12