Contents

lapexample.m

From A First Course in Machine Learning, Chapter 4. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] The Laplace approximation to a gamma density

clear all;close all;

Define the gamma parameters

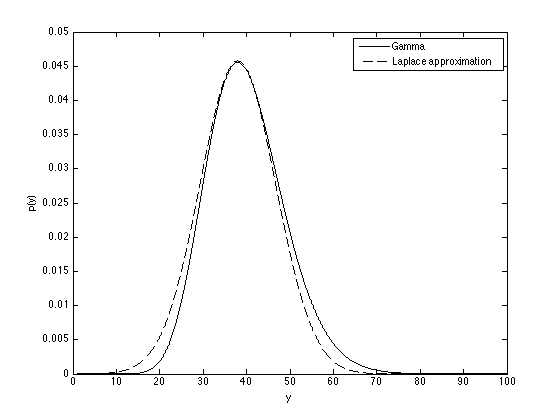
alpha = 20;
beta = 0.5;

% Find the mode
y_hat = (alpha-1)/beta;
% Find the variance
ss = (alpha-1)/beta^2;

Plot the gamma and the approximate Gaussian

y = [0:0.01:100];
figure(1);hold off
plot(y,gampdf(y,alpha,1/beta),'k'); %Note: Matlab uses an alternative parameterisation of the gamma function, hence the 1/beta.
hold on
plot(y,normpdf(y,y_hat,sqrt(ss)),'k--');
xlabel('y');
ylabel('p(y)');
legend('Gamma','Laplace approximation');

Second example

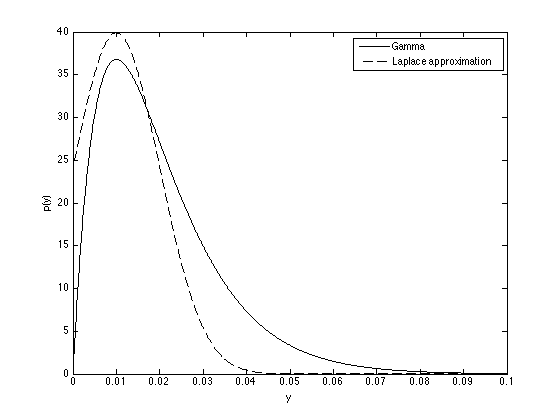
alpha = 2;
beta = 100;

% Find the mode
y_hat = (alpha-1)/beta;
% Find the variance
ss = (alpha-1)/beta^2;

y = [0:0.0001:0.1];
figure(1);hold off
plot(y,gampdf(y,alpha,1/beta),'k'); %Note: Matlab uses an alternative parameterisation of the gamma function, hence the 1/beta.
hold on
plot(y,normpdf(y,y_hat,sqrt(ss)),'k--');
xlabel('y');
ylabel('p(y)');
legend('Gamma','Laplace approximation');

Published with MATLAB® 7.12