Contents

mhexample.m

From A First Course in Machine Learning, Chapter 4. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] Example of Metropolis-Hastings

clear all;close all;
path(path,'../utilities');

Define the true density as a Gaussian

mu = [2;3];
si = [1 0.6;0.6 1];

Initialise sampler

x = rand(2,1);
x = [4;0.5];

Do N steps

fig1 = figure(1);hold off
% Plot the contours
[Xv,Yv] = meshgrid(0:0.1:5,0:0.1:5);
const = -log(2*pi) - log(det(si));
temp = [Xv(:)-mu(1) Yv(:)-mu(2)];
Probs = const - 0.5*diag(temp*inv(si)*temp');
contour(Xv,Yv,reshape(exp(Probs),size(Xv)),'k');
hold on
plot(x(1),x(2),'ko','markersize',10);
N = 40; % Increase this to generate more samples
jump_si = [0.5 0;0 0.5]; % Covariance of jumping Gaussian - try varying this and looking at the proportion of rejections/acceptances
Naccept = 0;


% Following lines make a movie uncomment them and the lines labels movie
% below
% winsize = get(fig1,'Position');
% winsize(1:2) = [0 0];
% numframes = N;
% A = moviein(numframes,fig1,winsize);

for n = 1:N
    % Propose a new value
    xs = gausssamp(x,jump_si,1)'; % Using a Gaussian jump, jump ratios cancel
    % Compute ratio of densities (done in log space, constants cancel)
    pnew = -0.5*(xs-mu)'*inv(si)*(xs-mu);
    pold = -0.5*(x-mu)'*inv(si)*(x-mu);
    plot(xs(1),xs(2),'ko','markersize',5,'markerfacecolor','k');
    if rand<=exp(pnew-pold)
        % Accept the sample
        plot([x(1) xs(1)],[x(2) xs(2)],'k','color',[0.6 0.6 0.6]);
        x = xs;
        Naccept = Naccept + 1;
    else
        plot([x(1) xs(1)],[x(2) xs(2)],'r--','color',[1 0.6 0.6]);
    end

    % Movie
%     A(:,n) = getframe(fig1,winsize);
end
legend('Posterior','Start','Samples')
fprintf('\nDashed lines show rejections');
fprintf('\nAcceptance ratio: %g',Naccept/N);

Dashed lines show rejections
Acceptance ratio: 0.675

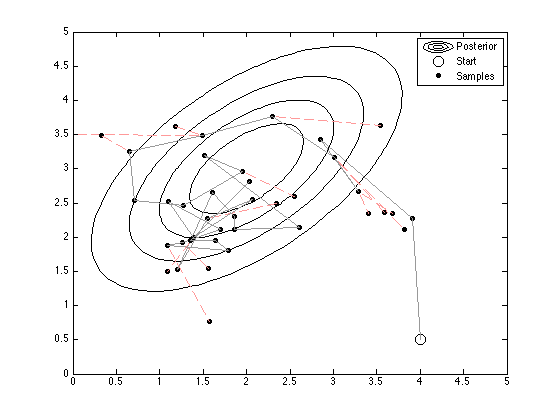
Watch the movie

movie(fig1,A,30,3,winsize);

Published with MATLAB® 7.12