Contents

svmgauss.m

From A First Course in Machine Learning, Chapter 4. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] SVM with Gaussian kernel

clear all;close all;

Load the data

load ../data/SVMdata2
% Put in class order for visualising the kernel
[t I] = sort(t);
X = X(I,:);

Plot the data

ma = {'ko','ks'};
fc = {[0 0 0],[1 1 1]};
tv = unique(t);
figure(1); hold off
for i = 1:length(tv)
    pos = find(t==tv(i));
    plot(X(pos,1),X(pos,2),ma{i},'markerfacecolor',fc{i});
    hold on
end

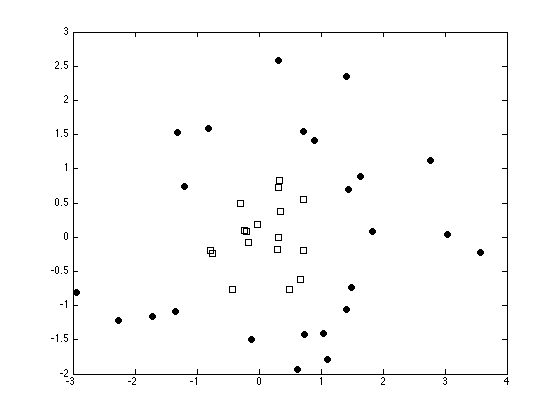
Compute Kernel and test Kernel

[Xv Yv] = meshgrid(-3:0.1:3,-3:0.1:3);
testX = [Xv(:) Yv(:)];
N = size(X,1);
Nt = size(testX,1);
K = zeros(N);
testK = zeros(N,Nt);

% Set kernel parameter
gamvals = [0.01 1 5 10 50];
for gv = 1:length(gamvals)

    gam = gamvals(gv);

    for n = 1:N
        for n2 = 1:N
            K(n,n2) = exp(-gam*sum((X(n,:)-X(n2,:)).^2));
        end
        for n2 = 1:Nt
            testK(n,n2) = exp(-gam*sum((X(n,:)-testX(n2,:)).^2));
        end
    end
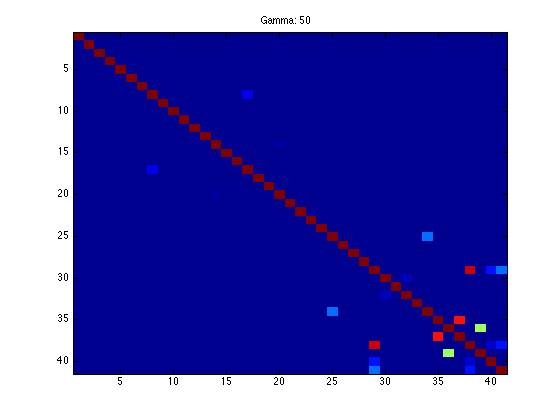
    figure(1);hold off
    imagesc(K);
    ti = sprintf('Gamma: %g',gam);
    title(ti);
    % Construct the optimisation
    H = (t*t').*K + 1e-5*eye(N);
    f = repmat(1,N,1);
    A = [];b = [];
    LB = repmat(0,N,1); UB = repmat(inf,N,1);
    Aeq = t';beq = 0;

    % Fix C
    C = 10;
    UB = repmat(C,N,1);
    % Following line runs the SVM
    alpha = quadprog(H,-f,A,b,Aeq,beq,LB,UB);

    fout = sum(repmat(alpha.*t,1,N).*K,1)';
    pos = find(alpha>1e-6);
    bias = mean(t(pos)-fout(pos));

    % Compute the test predictions
    testpred = (alpha.*t)'*testK + bias;
    testpred = testpred';

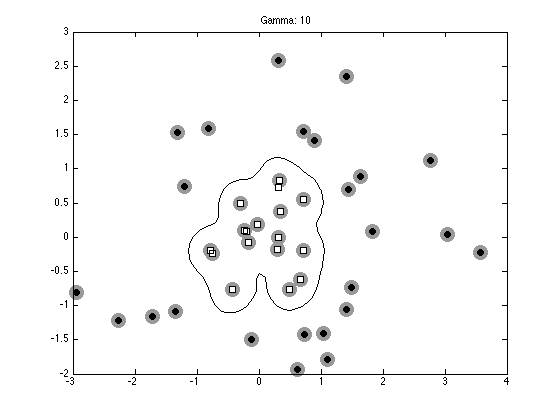
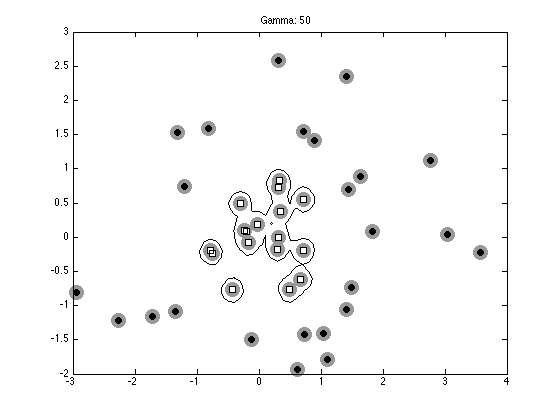
    % Plot the data, support vectors and decision boundary
    figure(2);hold off
    pos = find(alpha>1e-6);
    plot(X(pos,1),X(pos,2),'ko','markersize',15,'markerfacecolor',[0.6 0.6 0.6],...
        'markeredgecolor',[0.6 0.6 0.6]);
    hold on
    for i = 1:length(tv)
        pos = find(t==tv(i));
        plot(X(pos,1),X(pos,2),ma{i},'markerfacecolor',fc{i});
    end
    contour(Xv,Yv,reshape(testpred,size(Xv)),[0 0],'k');
    ti = sprintf('Gamma: %g',gam);
    title(ti);

Optimization terminated.

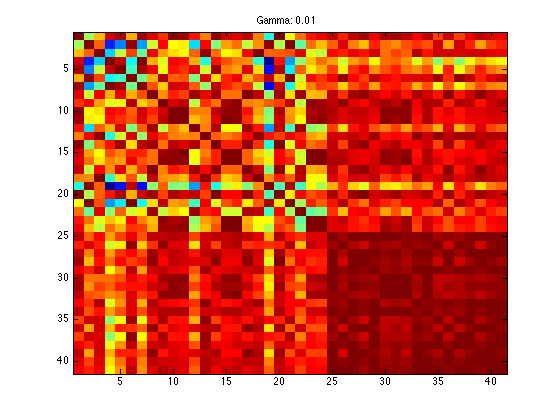
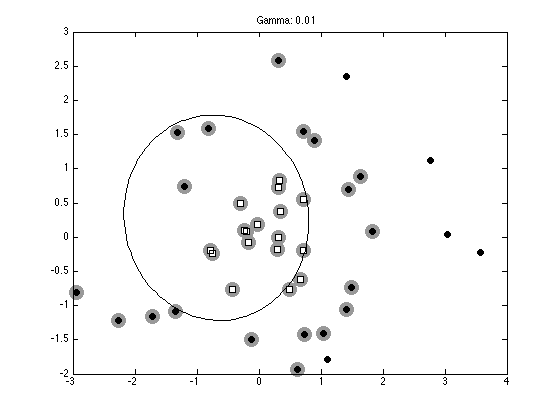
Optimization terminated.

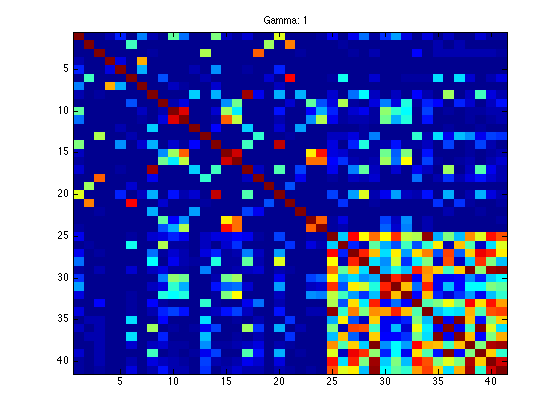
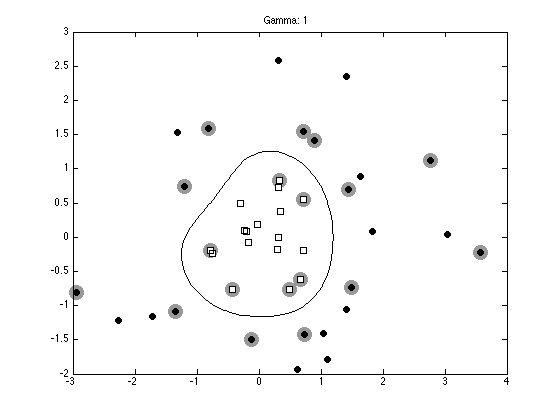
Optimization terminated.

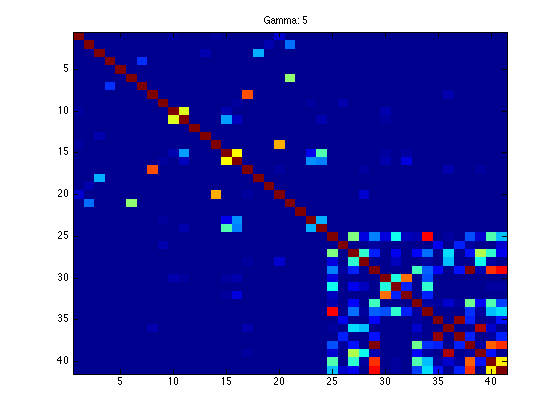
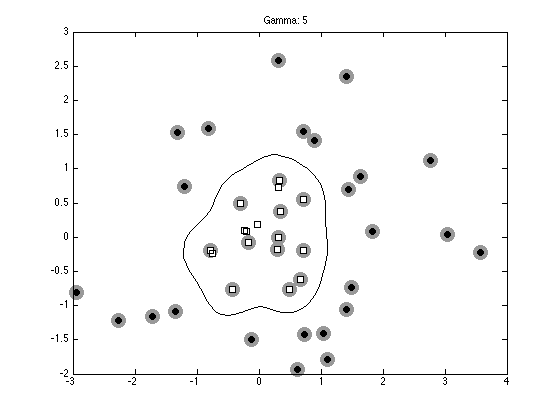
Optimization terminated.

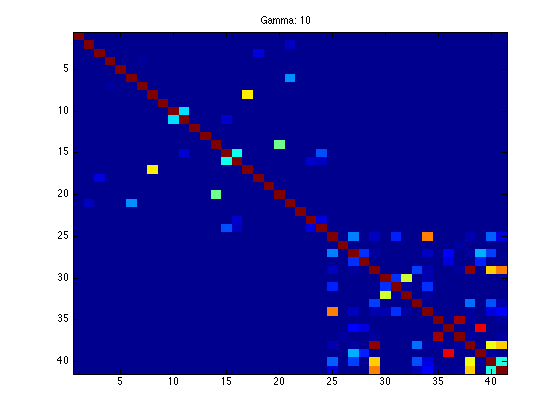
Optimization terminated.

end

Published with MATLAB® 7.13