Contents

svmhard.m

From A First Course in Machine Learning, Chapter 4. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] Hard margin SVM

clear all;close all;

Generate the data

x = [randn(20,2);randn(20,2)+4];
t = [repmat(-1,20,1);repmat(1,20,1)];

Plot the data

ma = {'ko','ks'};
fc = {[0 0 0],[1 1 1]};
tv = unique(t);
figure(1); hold off
for i = 1:length(tv)
    pos = find(t==tv(i));
    plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
    hold on
end

Setup the optimisation problem

N = size(x,1);
K = x*x';
H = (t*t').*K + 1e-5*eye(N);
f = repmat(1,N,1);
A = [];b = [];
LB = repmat(0,N,1); UB = repmat(inf,N,1);
Aeq = t';beq = 0;

% Following line runs the SVM
alpha = quadprog(H,-f,A,b,Aeq,beq,LB,UB);
% Compute the bias
fout = sum(repmat(alpha.*t,1,N).*K,1)';
pos = find(alpha>1e-6);
b = mean(t(pos)-fout(pos));

Warning: Trust-region-reflective algorithm does not solve this type of problem, using
active-set algorithm. You could also try the interior-point-convex algorithm: set the
Algorithm option to interior-point-convex and rerun. For more help, see Choosing the Algorithm
in the documentation. 
Optimization terminated.

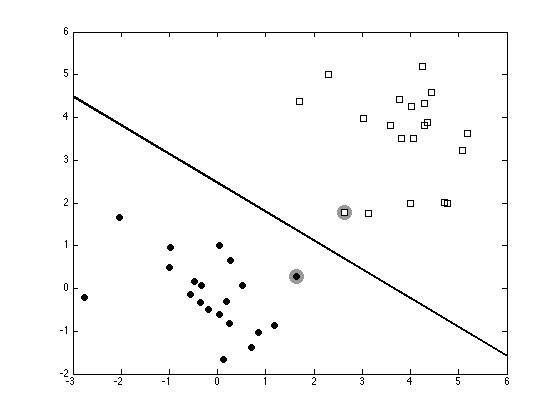
Plot the data, decision boundary and Support vectors

figure(1);hold off
pos = find(alpha>1e-6);
plot(x(pos,1),x(pos,2),'ko','markersize',15,'markerfacecolor',[0.6 0.6 0.6],...
    'markeredgecolor',[0.6 0.6 0.6]);
hold on
for i = 1:length(tv)
    pos = find(t==tv(i));
    plot(x(pos,1),x(pos,2),ma{i},'markerfacecolor',fc{i});
end

xp = xlim;
% Because this is a linear SVM, we can compute w and plot the decision
% boundary exactly.
w = sum(repmat(alpha.*t,1,2).*x,1)';
yp = -(b + w(1)*xp)/w(2);
plot(xp,yp,'k','linewidth',2)

Published with MATLAB® 7.13