Contents

gmixcv.m

From A First Course in Machine Learning, Chapter 6. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] Fitting a Gaussian mixture

clear all;close all;
path(path,'../utilities');

Load the data

load ../data/kmeansdata

Plot the data

figure(1);hold off
plot(X(:,1),X(:,2),'ko');

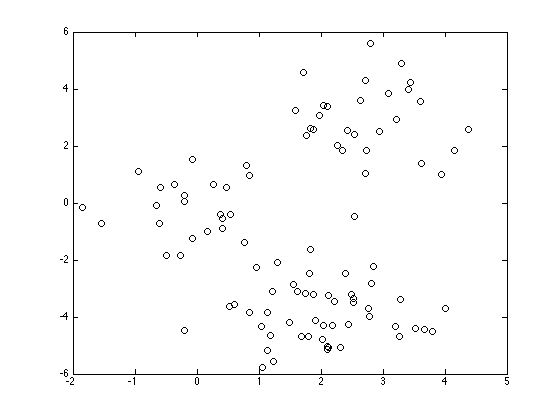
Do a 10-fold CV

NFold = 10;
N = size(X,1);
sizes = repmat(floor(N/NFold),1,NFold);
sizes(end) = sizes(end) + N - sum(sizes);
csizes = [0 cumsum(sizes)];
order = randperm(N); % Randomise the data order
MaxIts = 100;

Loop over K

Kvals = 1:10;
for kv = 1:length(Kvals)
    K = Kvals(kv);
    for fold = 1:NFold
        fprintf('\nK: %g, fold: %g',K,fold);
        foldindex = order(csizes(fold)+1:csizes(fold+1));
        trainX = X;
        trainX(foldindex,:) = [];
        testX = X(foldindex,:);

        % Train the mixture
        means = randn(K,2);
        for k = 1:K
            covs(:,:,k) = rand*eye(2);
        end
        priors = repmat(1/K,1,K);
        B = [];
        B(1) = -inf;
        converged = 0;
        it = 0;
        tol = 1e-2;
        Ntrain = size(trainX,1);
        D = size(X,2);
        while 1
            it = it + 1;
            % Update q
            temp = zeros(Ntrain,K);
            for k = 1:K
                const = -(D/2)*log(2*pi) - 0.5*log(det(covs(:,:,k)));
                Xm = trainX - repmat(means(k,:),Ntrain,1);
                temp(:,k) = const - 0.5 * diag(Xm*inv(covs(:,:,k))*Xm');
            end

            % Compute the Bound on the likelihood
            if it>1
                B(it) = sum(sum(q.*log(repmat(priors,Ntrain,1)))) + ...
                    sum(sum(q.*temp)) - ...
                    sum(sum(q.*log(q)));
                if abs(B(it)-B(it-1))<tol
                    converged = 1;

                end
            end

            if converged == 1 || it>MaxIts
                break
            end

            temp = temp + repmat(priors,Ntrain,1);

            q = exp(temp - repmat(max(temp,[],2),1,K));
            % Minor hack for numerical issues - stops the code crashing when
            % clusters are empty
            q(q<1e-3) = 1e-3;
            q(q>1-1e-3) = 1-1e-3;
            q = q./repmat(sum(q,2),1,K);
            % Update priors
            priors = mean(q,1);
            % Update means
            for k = 1:K
                means(k,:) = sum(trainX.*repmat(q(:,k),1,D),1)./sum(q(:,k));
            end
            % update covariances
            for k = 1:K
                Xm = trainX - repmat(means(k,:),Ntrain,1);
                covs(:,:,k) = (Xm.*repmat(q(:,k),1,D))'*Xm;
                covs(:,:,k) = covs(:,:,k)./sum(q(:,k));
            end


        end



        % Compute the held-out likelihood
        Ntest = size(testX,1);
        temp = zeros(Ntest,K);
        for k = 1:K
            const = -(D/2)*log(2*pi) - 0.5*log(det(covs(:,:,k)));
                Xm = testX - repmat(means(k,:),Ntest,1);
                temp(:,k) = const - 0.5 * diag(Xm*inv(covs(:,:,k))*Xm');

        end
        temp = exp(temp).*repmat(priors,Ntest,1);
        outlike(kv,csizes(fold)+1:csizes(fold+1)) = log(sum(temp,2))';


    end
end

K: 1, fold: 1
K: 1, fold: 2
K: 1, fold: 3
K: 1, fold: 4
K: 1, fold: 5
K: 1, fold: 6
K: 1, fold: 7
K: 1, fold: 8
K: 1, fold: 9
K: 1, fold: 10
K: 2, fold: 1
K: 2, fold: 2
K: 2, fold: 3
K: 2, fold: 4
K: 2, fold: 5
K: 2, fold: 6
K: 2, fold: 7
K: 2, fold: 8
K: 2, fold: 9
K: 2, fold: 10
K: 3, fold: 1
K: 3, fold: 2
K: 3, fold: 3
K: 3, fold: 4
K: 3, fold: 5
K: 3, fold: 6
K: 3, fold: 7
K: 3, fold: 8
K: 3, fold: 9
K: 3, fold: 10
K: 4, fold: 1
K: 4, fold: 2
K: 4, fold: 3
K: 4, fold: 4
K: 4, fold: 5
K: 4, fold: 6
K: 4, fold: 7
K: 4, fold: 8
K: 4, fold: 9
K: 4, fold: 10
K: 5, fold: 1
K: 5, fold: 2
K: 5, fold: 3
K: 5, fold: 4
K: 5, fold: 5
K: 5, fold: 6
K: 5, fold: 7
K: 5, fold: 8
K: 5, fold: 9
K: 5, fold: 10
K: 6, fold: 1
K: 6, fold: 2
K: 6, fold: 3
K: 6, fold: 4
K: 6, fold: 5
K: 6, fold: 6
K: 6, fold: 7
K: 6, fold: 8
K: 6, fold: 9
K: 6, fold: 10
K: 7, fold: 1
K: 7, fold: 2
K: 7, fold: 3
K: 7, fold: 4
K: 7, fold: 5
K: 7, fold: 6
K: 7, fold: 7
K: 7, fold: 8
K: 7, fold: 9
K: 7, fold: 10
K: 8, fold: 1
K: 8, fold: 2
K: 8, fold: 3
K: 8, fold: 4
K: 8, fold: 5
K: 8, fold: 6
K: 8, fold: 7
K: 8, fold: 8
K: 8, fold: 9
K: 8, fold: 10
K: 9, fold: 1
K: 9, fold: 2
K: 9, fold: 3
K: 9, fold: 4
K: 9, fold: 5
K: 9, fold: 6
K: 9, fold: 7
K: 9, fold: 8
K: 9, fold: 9
K: 9, fold: 10
K: 10, fold: 1
K: 10, fold: 2
K: 10, fold: 3
K: 10, fold: 4
K: 10, fold: 5
K: 10, fold: 6
K: 10, fold: 7
K: 10, fold: 8
K: 10, fold: 9
K: 10, fold: 10

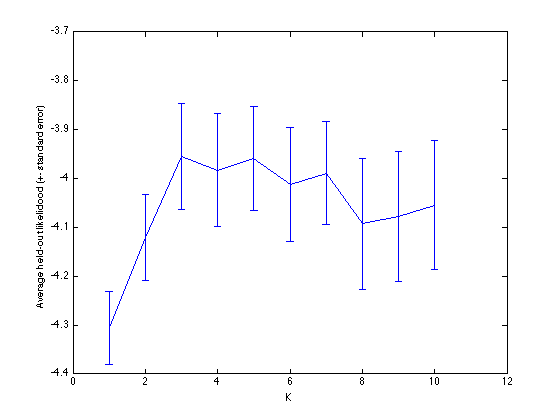
Plot the evolution in log likelihood

errorbar(Kvals,mean(outlike,2),std(outlike,1,2)./sqrt(N));
xlabel('K');
ylabel('Average held-out likelidood (+- standard error)');

Published with MATLAB® 7.13