Contents

ppcamvexample.m

From A First Course in Machine Learning, Chapter 6. Simon Rogers, 01/11/11 [simon.rogers@glasgow.ac.uk] Probabilistic PCA example using Variational Bayes with missing values

clear all;close all;

Generate the data

Y = [randn(20,2);randn(20,2)+5;randn(20,2)+repmat([5 0],20,1);randn(20,2)+repmat([0 5],20,1)];
% Add 5 random dimensions
N = size(Y,1);
Y = [Y randn(N,5)];
% labels - just used for plotting
t = [repmat(1,20,1);repmat(2,20,1);repmat(3,20,1);repmat(4,20,1)];

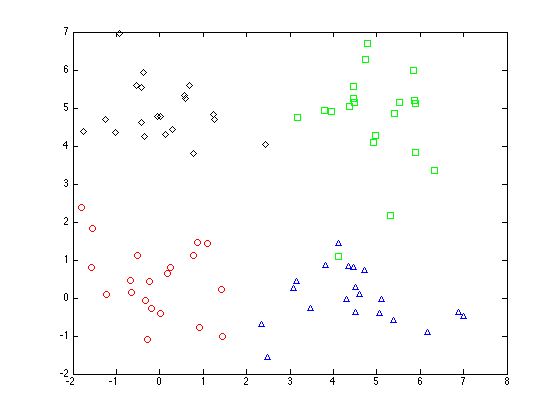
Plot the original data

symbs = {'ro','gs','b^','kd'};
figure(1);hold off
for k = 1:4
    pos = find(t==k);
    plot(Y(pos,1),Y(pos,2),symbs{k});
    hold on
end

Remove some values

[N,M] = size(Y);
Z = rand(N,M)<0.9; % I.e. 10 percent missing - try changing this
order = randperm(N);
Z(order(1),1:2) = [0 0]; % Make sure at least one has two missing in first two dimensions.

Initialise the parameters

a = 1;b = 1; % Hyper-parameters for precision
e_tau = a/b;
D = 2; % Number of projection dimensions
e_w = randn(M,D);
for m = 1:M
    e_wwt(:,:,m) = eye(D) + e_w(m,:)'*e_w(m,:);
end
tol = 1e-3;
e_tau = 1;

Run the algorithm

Mean center the data (for visualisation later)

Y = Y - repmat(mean(Y,1),N,1);
MaxIts = 100;
for it = 1:MaxIts
    % Update X
    % Compute \Sigma_x - this is the same for all x

    for n = 1:N
        sigx(:,:,n) = inv(eye(D) + e_tau*sum(e_wwt.*repmat(reshape(Z(n,:),[1 1 M]),[D D 1]),3));
        e_X(n,:) = e_tau*sigx(:,:,n)*sum(e_w.*repmat((Z(n,:).*Y(n,:)),D,1)',1)';
        e_XXt(:,:,n) = sigx(:,:,n) + e_X(n,:)'*e_X(n,:);
    end

    % Update W

    for m = 1:M
        sigw(:,:,m) = inv(eye(D) + e_tau*sum(e_XXt.*repmat(reshape(Z(:,m),[1 1 N]),[D D 1]),3));
        e_w(m,:) = e_tau*sigw(:,:,m)*sum(e_X.*repmat((Z(:,m).*Y(:,m)),1,D),1)';
        e_wwt(:,:,m) = sigw(:,:,m) + e_w(m,:)'*e_w(m,:);
    end

    % Update tau
    e = a + sum(sum(Z))/2;
    % Compute the nasty outer expectation.  Note that these two loops could
    % be made *much* more efficient
    outer_expect = 0;
    for n = 1:N
        for m = 1:M
            outer_expect = outer_expect + Z(n,m)*(...
                trace(e_wwt(:,:,m)*sigx(:,:,n)) + ...
                e_X(n,:)*e_wwt(:,:,m)*e_X(n,:)');
        end
    end
    f = b + 0.5*sum(sum(Z.*(Y.^2))) - sum(sum(Z.*(e_X*e_w'))) + ...
        0.5*outer_expect;
    e_tau = e/f;
    e_log_tau = mean(log(gamrnd(e,1/f,[1000,1])));


    % Compute the bound
    LB = a*log(b) + (a-1)*e_log_tau - b*e_tau - gammaln(a);
    LB = LB - (e*log(f) + (e-1)*e_log_tau - f*e_tau - gammaln(e));


    for n = 1:N
        LB = LB + (...
            -(D/2)*log(2*pi) - 0.5*(trace(sigx(:,:,n)) + e_X(n,:)*e_X(n,:)'));
        LB = LB - (...
            -(D/2)*log(2*pi) - 0.5*log(det(sigx(:,:,n))) - 0.5*D);
    end

    for m = 1:M
        LB = LB + (...
            - (D/2)*log(2*pi) - 0.5*(trace(sigw(:,:,m)) + e_w(m,:)*e_X(m,:)'));
        LB = LB - (...
            -(D/2)*log(2*pi) - 0.5*log(det(sigw(:,:,m))) - 0.5*D);
    end

    outer_expect = 0;
    for n = 1:N
        for m = 1:M
            outer_expect = outer_expect + Z(n,m)*(trace(e_wwt(:,:,m)*sigx(:,:,n)) + e_X(n,:)*e_wwt(:,:,m)*e_X(n,:)');
        end
    end

    % likelihood bit
    LB = LB + (...
        -(N*M/2)*log(2*pi) + (N*M/2)*e_log_tau - ...
        0.5*e_tau*(sum(sum(Z.*Y.^2)) - 2*sum(sum(Z.*Y.*(e_w*e_X')')) + outer_expect));
    B(it) = LB;

    if it>2
        if abs(B(it)-B(it-1))<tol
            break
        end
    end
end

Plot the bound

figure(1);hold off
plot(B);
xlabel('Iterations');
ylabel('Bound');

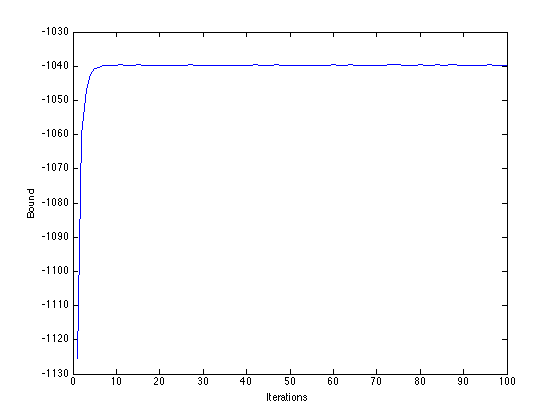
Plot the projection

figure(1);hold off
for k = 1:4
    pos = find(t==k);
    plot(e_X(pos,1),e_X(pos,2),symbs{k});
    hold on
end
title('Projection');

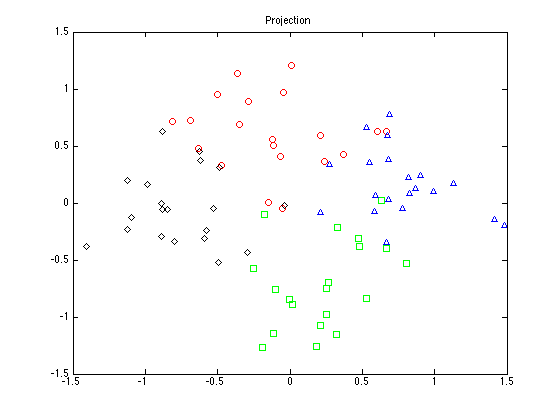
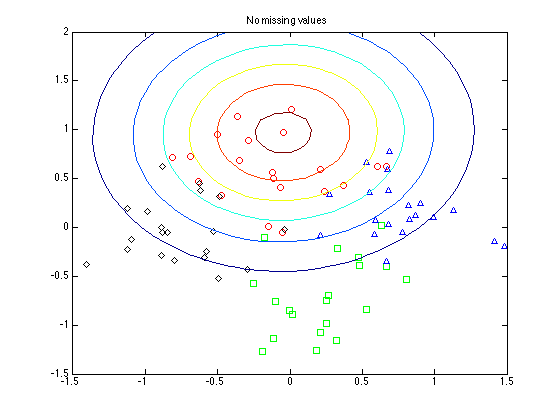
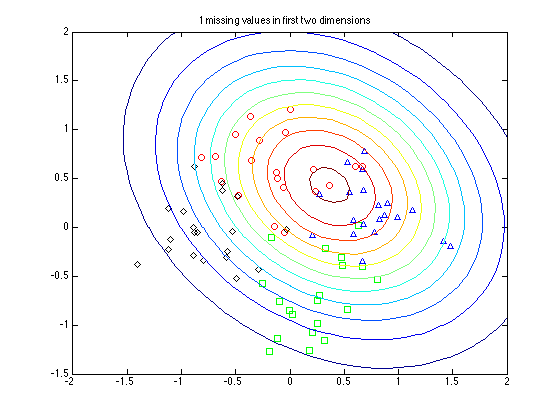
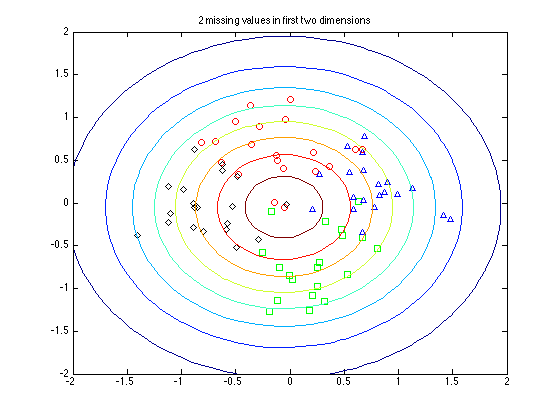
Find something with nothing missing, something with one value missing and something with two values

Uncertainty increases as more values in the first two dimensions are missing.

path(path,'../utilities');
s = sum(Z(:,1:2)==0,2);
figure(1);hold off
for k = 1:4
    pos = find(t==k);
    plot(e_X(pos,1),e_X(pos,2),symbs{k});
    hold on
end
pos = find(s==0);
pos = pos(1);
plot_2D_gauss(e_X(pos,:),sigx(:,:,pos),[-2:0.1:2],[-2:0.1:2]);
title('No missing values');

figure(2);hold off
for k = 1:4
    pos = find(t==k);
    plot(e_X(pos,1),e_X(pos,2),symbs{k});
    hold on
end
pos = find(s==1);
pos = pos(1);
plot_2D_gauss(e_X(pos,:),sigx(:,:,pos),[-2:0.1:2],[-2:0.1:2]);
title('1 missing values in first two dimensions');

figure(3);hold off
for k = 1:4
    pos = find(t==k);
    plot(e_X(pos,1),e_X(pos,2),symbs{k});
    hold on
end
pos = find(s==2);
pos = pos(1);
plot_2D_gauss(e_X(pos,:),sigx(:,:,pos),[-2:0.1:2],[-2:0.1:2]);
title('2 missing values in first two dimensions');

Published with MATLAB® 7.13