Contents

gpprior.m

Plots realisations from a GP prior using an RBF covariance function

From A First Course in Machine Learning Simon Rogers, August 2016 [simon.rogers@glasgow.ac.uk]

clear all; close all;

Define the x variable

The first step is to define the x values of interest, we'll pick some random ones in the range -5 to 5

x = rand(200,1) * 10 - 5;
x = sort(x);

Define the kernel parameters of interest

We are using an RBF covariance function:

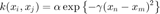
$$k(x_i,x_j) = \alpha\exp\left\{-\gamma(x_n-x_m)^2\right\}$$

gamvals = [0.05,0.1,0.5];
alpha = 1;

Loop over the gamma values

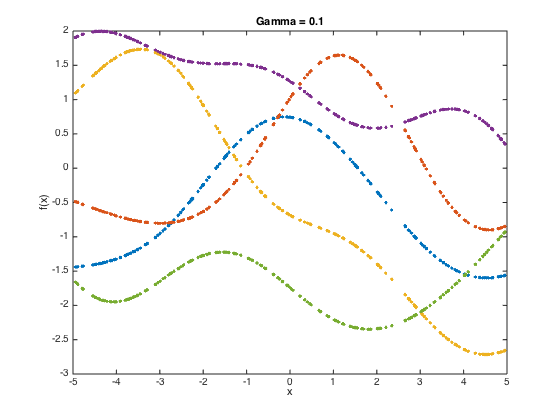
at each stage, compute the covariance matrix and then sample 5 functions from the GP (i.e. 5 realisations from the N dimensional Gaussian with men zero and covariance equal to the covariance matrix.

N = length(x);
for gam = gamvals
    C = zeros(N);
    for n = 1:N
        for n2 = 1:N
            C(n,n2) = alpha*exp(-gam*(x(n)-x(n2))^2);
        end
    end
    % add some jitter for numerical stability
    C = C + 1e-6*eye(N);
    f = mvnrnd(repmat(0,N,1),C,5);
    figure()
    plot(x,f,'.');
    title(sprintf('Gamma = %g',gam));
    xlabel('x');
    ylabel('f(x)');
    drawnow;
end


Published with MATLAB® R2014b