state_chain

state_chain.m
Define the transition probabilities
Initialise some things
Do the sampling
Plot the resulting probabilities
Check detailed balance

state_chain.m

Sampling from the simple state space model as an example of MCMC Here we try a different proposal to make sure it still works!

From A First Course in Machine Learning Simon Rogers, August 2016 [simon.rogers@glasgow.ac.uk]

clear all; close all;

Define the transition probabilities

Each row defines the probabilities of going from a state Here we will make a random one

tran = rand(5,5);
tran = tran./repmat(sum(tran,2),1,5);

Initialise some things

The initial state

x = 2;
% The number of samples
S = 2000;
% The probabilities
p = [0.1 0.1 0.4 0.2 0.2];
% A vector to store all sampled states
allx = zeros(S,1);

Do the sampling

for s = 1:S
    % Propose new according to transition matrix
    newx = find(rand<=cumsum(tran(x,:)),1);
    met_ratio = p(newx)/p(x);
    % Proposal is no longer symmetric so we have to include the second term
    met_ratio = met_ratio * tran(newx,x)/tran(x,newx);
    if rand<=met_ratio
        x = newx;
    end
    allx(s) = x;
end

Plot the resulting probabilities

figure(1);hold off
[a,b] = hist(allx,1:5);
a = a./S;
c = bar([1:5],[a' p']);
set(c(1),'facecolor',[0 0 0])
set(c(2),'facecolor',[0.6 0.6 0.6])
legend('Sampled','True')

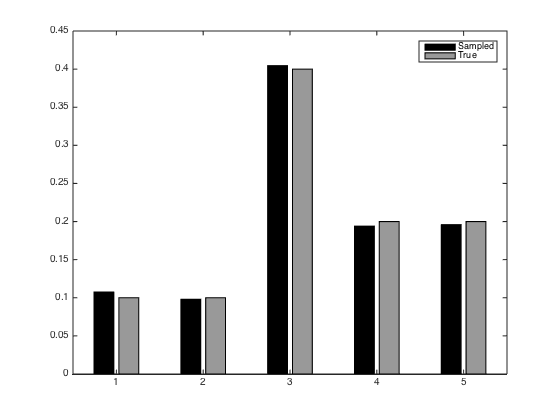
Check detailed balance

The number of 1,2 in the sequence should be the same (roughly) as the number of 2,1

sum(allx(1:end-1)==1 & allx(2:end)==2)
sum(allx(1:end-1)==2 & allx(2:end)==1)
% Ditto 2,3 and 3,2
sum(allx(1:end-1)==2 & allx(2:end)==3)
sum(allx(1:end-1)==3 & allx(2:end)==2)