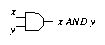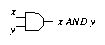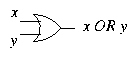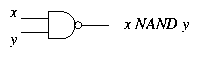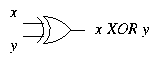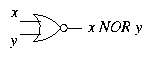Digital Logic and Truth Tables
Digital Logic and Truth Tables
Information Processing Operations
How is digital information processed and manipulated?
We start with some fundamental operations on binary digits and work up
to more complicated operations.
AND
If x and y are binary digits (either 0 or 1) then
is a
binary digit, defined by
More explicitly, AND is defined by the table
Diagrammatically:
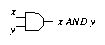
The electronic component which implements the AND operation is
called an AND gate.
Truth Tables
Instead of 0 and 1, the binary values are sometimes referred to as
false and true. The AND operation then has the same
meaning as in ordinary language: x AND y is true if x is true
and y is true.
The table defining AND is usually called a truth table, and
can be written out using false and true instead of 0 and 1.
Yet another terminology is high and low for 1 and 0,
referring to high and low voltage levels in electronics. We will use
all these terms interchangeably, but we will normally stick to 0 and
1 when writing out truth tables.
OR
If x and y are binary digits (either 0 or 1) then
is a
binary digit, defined by
|
|
| | | | |
if x = 1 or y = 1 or both |
|
| | | | |
|
|
|
The truth table for OR is as follows.
Again, note that OR has the same meaning as in ordinary language:
x OR y is true (i.e. 1) if x is true or y is true (or both).
Diagrammatically:
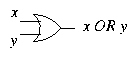
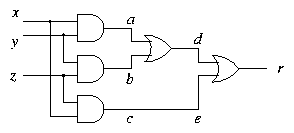
Example: Majority Voting
Imagine that three people have to vote either Yes (represented by 1)
or No (represented by 0). The overall result is the majority decision.
If x, y, z stand for the three votes, and r stands for the
result, then we can write
|
r = (x AND y) OR (y AND z) OR (z AND x) |
|
Diagrammatically:
NOT
It turns out that AND and OR are not sufficient to define all
functions on binary digits. The missing ingredient is the NOT
operation.
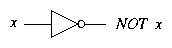
Again, if we think in terms of truth values, NOT has its familiar meaning.
A NOT gate is often called an inverter.
By using AND , OR and NOT in combination, it is possible to
define any desired function on binary numbers - for example,
addition or multiplication. We will see how to do this in a few
lectures' time.
Perhaps surprisingly, we only need NOT and just one of AND
and OR . We can check that the circuit
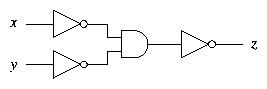
calculates z = x OR y.
One Fundamental Operation
Even more remarkably, it is possible to build up all functions from
combinations of just one operation: the NAND operation, defined by
and drawn like this:
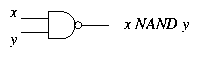
You can check that
|
x NAND y = NOT (x AND y). |
|
Assuming that we have NAND but not AND , OR or NOT , we can
define the other operations as follows:
XOR
In English, it is not always clear whether ``A or B'' means ``A or B
or possibly both'' or ``either A or B but not both''. As we have seen,
the logical operation OR has the first meaning; it is sometimes
called inclusive or.
The operation with the second meaning is exclusive or, written
XOR .
If x and y are binary digits (either 0 or 1) then
is a
binary digit, defined by
|
|
| | | | |
if either x = 1 or y = 1 but not both |
|
| | | | |
|
|
|
The truth table for XOR is as follows.
Diagrammatically:
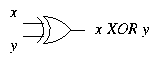
Another Fundamental Operation
Just as NAND is defined by
|
x NAND y = NOT (x AND y), |
|
we can also define an operation called NOR by
Its truth table is as follows.
It is drawn like this:
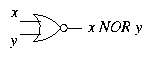
Like NAND , NOR can be used to define all the other operations.
Exercise: Check these equations.
Truth Table Exercise
For practice in calculating the output from a circuit, use the TruthTable exercise.
This exercise can be found at the following page : TruthTable Exercise
File translated from
TEX
by
TTH,
version 2.78.
On 27 Jul 2001, 10:19.