Paul Cockshott
Following the early suggestion by Deutsch [6], there has been considerable discussion in the literature of the possibility of building quantum computing machines. This has moved from basic discussion about the concept of such machines through studies of the mathematical properties of logic gates that might be adequate to build them[7] [10] [8][16], to discussions of practical algorithms that might be run on them [15]. Despite doubts that have been expressed about the physical practicability of quantum computers due to the problem of decoherence [14][5], there seems good reason to hope that these are soluble[9] in light of the development of quantum error correcting codes[2] [1]. Increasing numbers of practical suggestions for the technological implementation of quantum computers have been advanced ranging from the use of cold trapped ions [3] to the use of NMR technology [12].
Although conventional computers using semi-conductors rely upon quantum effects in their underlying technology, their design principles are classical. They have a definite state vector and they evolve deterministically between states in this space. Thus the state of a classical computer with an n bit store is defined by a position in an n dimensional binary co-ordinate state space.
In contrast the state of
a quantum computer with a store made up of n quantum two state
observables, or qubits, is given by a point in 
dimensional
Hilbert space. Each dimension of this space corresponds to one
of the possible values that n classical bits can assume.
These possible bit patterns constitute basis vectors for the Hilbert
space, and, associated with each such basis vector there is a complex
valued amplitude. At any instant the quantum computer is in a linear
superposition
of all of its possible bit patterns.
It is this ability to exist in multiple states at once that is
exploited by algorithms such as Shor's method of prime factorisation
[15].
If we abstract from the difficult technical problem of long term coherent storage of qubit vectors, this ability of the store to exist in multiple simultaneous states may be relevant to database compression.
In the well established relational model[4] data is
stored in relations or tables.
Given sets 
, (not necessarily distinct),
R is a relation on these n sets if it is a set of n-tuples each of which
has its first element from 
, its second element from 
, etc.
The set 
is known as the ith domain of R.
Each row in a database table represents a tuple of the relation.
The tuples are conventionally represented as a vector of bits
divided into fields 
where 
contains
a symbol, drawn from some binary encoded alphabet, corresponding
to an element of . If a single row can be encoded in
c bits and we have r rows, then the whole databse
occupies c.r bits.
In a quantum system a row could, using the same encoding, be represented in c qubits. However, use of superposition of states would allow a single vector of c qubits to represent all r rows, each with an appropriate amplitude. It is evident that were we to make a classical measurement on such a superposited tuple, we would only be able to read out one of the r rows of the database. The measurement would cause the wave function of the database to collapse onto one of its tuples.
The restriction of only being able to read out one tuple from the database can be evaded by using controled not gates as a means of copying the database before measuring it[8]. By sending the qubits of the tuple through the control input of a controlled not gate, and qubits prepared in state | 0> through the other as shown in Fig 1, one can create an `oracle' that acts as a stochastic generator of tuples from the database. By tailoring the amplitudes of the different tuples in the database one could tune the probabilities with which they would be read.
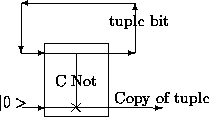
Figure 1: Use of controled not gate to copy the data before performing
classical measurement
Current uses of databases fall into two broad areas, transaction processing and management information. In the case of the former, the data are bearers of important social relations such as relative indebtedness, and, in consequence, it is of the utmost importance that the integrity and detail of the data be preserved. Were this not the case, there would be a danger that alterations of the data would result in changes in peoples' social status.
In the latter case, the data are used by organisations to make decisions about their future courses of action. Here, the information presented relates not to individual people, or individual economic transactions, but to collections of people and events. One is concerned not with what an individual student gained in her A Levels, but with the mean results in English A levels by region of the country, or the average sales of dishwashers over the last year by month and by model. The ultimate source, however, for the summary information so presented, are the original transactional records demanded by the relations in question.
There is however, an inherent mismatch between the transactional sources and the summary uses of management information. The sources are voluminous and accurate, the uses compact and, although this is not always appreciated, inherently approximate. This approximation arises from two causes. Firstly, the results presented : totals and averages, are arrived at by means of summation, an inherently information destroying operation. Secondly once one abstracts from their individuality, individual commercial transactions can be seen as stochastic events. The ability to directly model this could be an attractive feature of quantum databases.
In order to prepare tuples in an appropriate superposition
one needs a primitive operation that will combine the
state of two qubits into one. An operator capble of doing
this would be the MIX gate shown in Fig. 2.
This takes two qubits and A, and B. Bit A passes out unaffected as
A'. The second output is an equal mixture of the two input states
. The MIX gate can
be represented as the matrix:
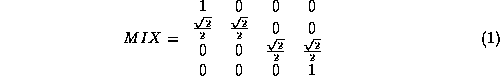
It is obviously possible to combine 
tuples into a superposition
by a MIX network of depth N.
The basic operations permited on a relation database are selection, projection and join [4].
Selection forms a new relation B out of all tuples in relation A that meet some
predicate. A particular case of selection uses equality against the primary key
of the relation, where the primary key is a column which, on its own, uniquely identifies
a tuple.
If primary key selection is performed as a classical operation after quantum measurement
one would need to perform at least 
operations to have a 50% chance
of encountering the tuple.
If, instead of being performed after classical measurement, the operation is
performed in the quantum domain, Grover [13] has shown that
primary key selection can be performed in 
steps. His technique
involves repeatedly inverting the phase of the selected word (tuple) and then inverting
the phases of all tuples about their average. The amplitude of the selected tuple
then goes approximately through the sequence
converging to an amplitude of 1 after 
cycles.
For the more general case of a selection which yields a set rather than a singleton
tuple, Grover's algorithm will concentrate the amplitude in 
the subset of the relation
R that meets predicate p in 
steps, where f is the fraction
of tuples meeting the selection criterion.
For primary key selection the quantum search procedure is inferior to the
use of a classical relational database with an index on the primary key, an
operation that costs 
. For generalised search operations that do
not lend themselves to indexing, it is superior.
Relational database projection can be achieved trivially in the quantum database by simply discarding all qubits other than those coding for the domains onto which the relation is projected. Relational projection here translates directly into a projection onto the appropriate sub-manifold of Hilbert space.
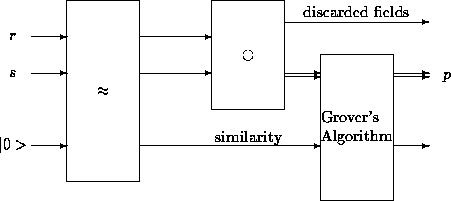
Figure 3: The join operation can be performed by composing a similarity operator 
,
a combining operator 
and Grover's algorithm
Let r,s be sets. Let
where
is the join functional, is some dyadic combining operator of type ( 
),
where is the type of the tuples in relation r etc. In
contemporary relational databases this usually involves some combination of
permutation and projection on the domains of the two relations, but analytically
the combining operator can be any function. is some similarity operator of type
( 0..1), two tuples v,u are said to be similar if 
.
Contemporary relational database systems usually support equijoin where
the similarity operator tests fields in the first and second tuple for
equality, but again, the analytical case is more general and any comparison
operation is allowed. In conventional databases the result of comparison is
boolean valued, but that is a special case arising from the fact that
a given tuple either is or is not present in the relation. In a quantum
relation the tuples are present with a complex amplitude, which, on measurement,
determines the probability of finding the tuple. One can thus see
two levels of generalisation of the similarity operation:
;then we can say that p contains an element corresponding to every pair of elements in x,y that are similar.
each such 
is the result of applying the combining operator to
the pairs of similar elements.
Let us define the conditional similarity 
of two quantum relations a,b
to be :
Where 
is the probability of tuple y in relation x.
This will be a number in the range 0..1.
We can use it to define the probabilities associated with elements of
a joined set.
Thus in (2) and (3) we have
Note that
The generalised join operation can be performed as shown in Fig. 3.
Its complexity is dominated by the Grover's Algorithm network used to boost the
amplitude of the similar joined components, whose complexity will be 
.
This contrasts with the complexity of generalised join on a classical computer of
where 
is the cardinality of relation s.
If we consider the worst case where the joined relation contains a single tuple,
and
, then the quantum computation takes the
square root of the number of steps of the classical one. Where the conditional similarity
is higher, the complexity advantage of the quantum computation is higher.
In the restricted case of equijoin using a primary key field of relation s, the
classical complexity is 
. Only when the relation s is
much larger than the relation r and 
tends to zero,
does this fall below the complexity of the quantum computation.
The approach given by Grover can be generalised to set an upper complexity limit to the basic operations of relational databases on a quantum computer. Except in special cases where indices can be used on a classical machine, the quantum upper complexity limit is lower than the classical one.
,